Work, energy and power

Definition of work

In the figure below, an object is pulled by a rope with a force $\vec F$. The object has moved with a displacement of $\vec d$. How much is the work done on the object by the force?

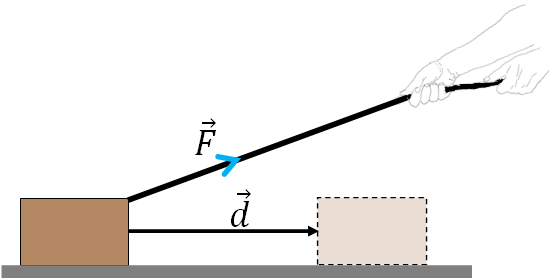
Work done by a constant force, $\vec F$ is defined as

$W=Fd\cos\theta$

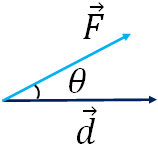
Note that the above equation is valid for any constant force. Constant force means, both the direction and the magnitude of the force do not change during the object's displacement.

If there is no displacement of the object, $d=0$, and the work, $W=0$.

When the force and the displacement are perpendicular to each other, θ = 90°, and the work is

$W=Fd \cos 90=0$

So, when the force is acting on the object in one direction and the object is moving in a direction perpendicular to the force, then there will be no work is done by the force. For example, if you walk on a horizontal surface, the force of gravity does no work on you as it acts perpendicular to your displacement.

SI Unit of work:

Work done by gravity and work against gravity

$W=F_g h\:\cos0=mgh$.

But when you lift an object, the gravity does a negative work on the object as the object moves opposite to the force of gravity.

If you raise an object by attaching a rope with it, then the lifting force is the force of tension on the rope. You can also place an object on your hand and lift it by raising your hand, here the force that raises the object is the normal force on the object by your hand. While the gravity does a negative work on the object, the lifting force does a positive work on the object as the lifting force and the object's displacement are in the same direction.

How much work is required to lift an object without acceleration?

Let us consider an object that is being raised by a rope. The force that raises the object is the force of tension on the rope, $F_t$.

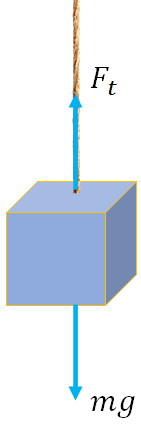
There are two forces acting on the object, $F_t$ in the upward direction and the force of gravity in the downward direction. When the object is lifted with a constant velocity, then the acceleration of the object is zero. And the force of tension balances the force of gravity,

$F_t=mg$

So, the work by $F_t$ is

$W=F_t h \cos 0=mgh$

This is the work required to lift an object to a height $h$.

Work done when you climb stairs or a ramp

$W=mgh$

where $h$ is the height of the stairs.

Note that, whether it is the work by gravity, work against gravity or the work required to climb a staircase or a ramp depends only on the height. For example, if you make a displacement on a ramp, you have two components of displacements as displacement is a vector: a vertical and a horizontal displacement. Work for the horizontal displacement is zero, as the force and this displacement are perpendicular to each other. So the work depends only on the vertical displacement, which is the height. The length of the ramp does not affect the work.

Work by friction

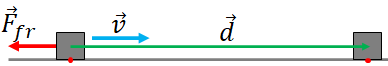
$W=F_{fr} d \cos180=-F_{fr}d$

$F_{fr}$ and $d$ are positive as they are the magnitudes of the friction force and the object's displacement. So, the work by friction is always negative.

Now let us consider, the object is moving on a path as shown below.

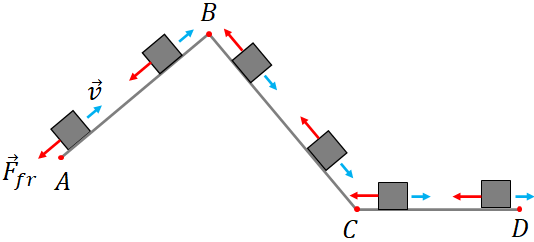
Here, the path is not a straight line instead there are three straight paths: AB, BC and CD. The initial and the final positions of the object are A and D. So, the displacement of the object is AD. Now, if you look at the direction of the friction force, it is not in one direction but is different for different paths. That is the force is not constant, and we cannot use the displacement AD to find the work. But you see that, in each straight path, the force is constant because at any point on the path, the direction of the force is the same. So, we can find the work in each straight path. Then if you add the work in each segment, we get the total work by friction.

Finding the work in each straight path and add them, we get

$W=-F_{fr}\, AB-F_{fr}\, BC-F_{fr}\, CD$

 $=-F_{fr}(AB+BC+CD)$

From the figure, you see that $AB+BC+CD$ is the total distance traveled by the object. So, we can write

$W=-F_{fr} d$, where $d$ is the distance traveled by the object.

Note that in the work by friction equation, $d$ is the distance, not the magnitude of the displacement. The above equation is valid for any path, which includes curved paths.

Energy

Kinetic energy

Work-Energy Principle

$W_{net}=\Delta KE$.

This is called work-energy principle or work-energy theorem. The derivation of this equation is given in a separate page, derivation-of-work-energy-principle.

Potential energy

Gravitational potential energy

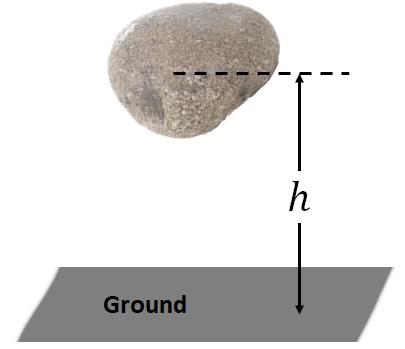
$PE_g=mgh$.

Elastic or spring potential energy

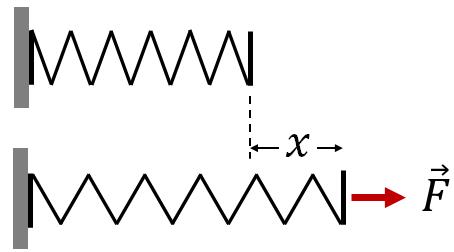
$F=kx$, where $k$ is the spring constant or force constant of the spring.

This force does a work on the spring. The work done to stretch or compress the spring is

$W=\dfrac{1}{2}kx^2$

Due to this work, the spring gains some energy, and that energy is called, spring potential energy or elastic potential energy.Therefore, elastic potential energy of a spring is

$PE_{spring}=\dfrac{1}{2}kx^2$.

Total mechanical energy

$Total \:Mechanical \: energy = PE + KE$

Conservative and nonconservative forces

But if a work by a force depends on the path of the object, then that force is called a nonconservative force. Since the work by friction depends on the path, friction is a nonconservative force.

Work and potential energy with conservative force

$W_c=-\Delta PE$

We can prove this by considering the work by gravity as force of gravity is a conservative force. Assume an object is at some height $y_1$. Now, you are lifting this object vertically upwards to a new vertical position, $y_2$. So, the vertical displacement of the object is

$h=y_2-y_1$

Finding the work by gravity,

$W=-mgh=-mg(y_2-y_1)$

 $=-(mg\,y_2-mg\,y_1)$

$mg\,y_1$ is the initial gravitational potential energy and $mg\,y_2$ is the final gravitational potential energy of the object. Therefore,

$W=-\Delta PE_G$

$W_c=-\Delta PE$

Total work on an object or a system of objects

$W_{net}=W_c+W_{nc}$

We have from work-energy theorem,

$W_{net}=\Delta KE$

And also we have

$W_c=-\Delta PE$

Substituting these in the net work equation,

$\Delta KE=-\Delta PE+W_{nc}$.

$\Delta (KE+PE)=W_{nc}$.

$\Delta E=W_{nc}$.

where $E=KE+PE$, is the total mechanical energy of the system.

Law of conservation of mechanical energy

$\Delta E=0$.

$E_{final}-E_{initial}=0$

$E_{initial}=E_{final}$

Law of conservation of energy

$\Delta E = W_{nc}$

If friction is the only nonconservative force acting on the system, then

$W_{nc}=W_{fr}$

We have the Work by friction that is

$W_{fr}=-F_{fr}d$, where $d $ is the distance traveled by the object under friction.

When friction does work on an object, heat is generated. Heat is a form of energy, so we call the generated heat thermal energy. The amount of thermal energy generated by friction is $F_{fr}d$.

Substituting $W_{nc}=W_{fr}=-F_{fr}d$ in the first equation, we get

$\Delta E = -F_{fr}d$

$E_{final}-E_{initial}=-F_{fr}d$

or

$E_{initial}=E_{final}+F_{fr}d$

On the left hand side of the equation, we have the initial mechanical energy, which is the total initial energy of the system. On the right hand side, the second term $F_{fr}d$, is the thermal energy. So, the part of the initial energy has now been transformed into thermal energy and the final mechanical energy is now lower than the initial mechanical energy. So, there is a transformation of energy but nothing is lost. That is the total energy is always conserved. This is called the law of conservation of energy, an important law of physics.

Power

$P=\dfrac{W}{t}$

Since, when work is done, energy is transformed, power is also the rate at which energy is transformed,i.e.,

$P=\dfrac{E}{t}$

where $E$ is the amount of energy transformed in a time interval, $t$.

SI Unit of power is watt (W) that is same as J/s.

If you look at the electric bulbs or other electric equipments, you can see its power rating. A 100 W bulb uses 100 J of energy in 1s. Electric utility services charge us for how much energy was used by our electric equipments.

If the work is done by a constant force, then

$P=\dfrac{Fd \cos\theta}{t}$

$ =F\,v \cos\theta$

where, $v=d/t$ is the magnitude of the object's velocity. If the object moves in the direction of the force, then $\theta =0$ and we have

$P=F\,v$

Horse power

The conversion factor from horse power to watt is

$1\,hp=746\,W$.