Static equilibrium and elasticity
Static equilibrium
Static equilibrium is the state of an object in rest. So, an object in static equilibrium has no translational or rotational motion. When building structures such as buildings and bridges, it is important to analyze their stability and load capacity. To analyze a structure, the forces and torques on the structure are calculated by assuming it in static equilibrium.Conditions for static equilibrium
Since an object in static equilibrium has no translational or rotational motion, there is no net force or net torque acting on the object. So, we have two conditions for static equilibrium, one is for the force and the other for the torque.Condition 1: Net force on the object is zero:
$\sum{\vec F}=0$
Note that the greek letter, sigma, $\sum$ is the symbol for the sum.
You know that force is a vector, and the components of a vector are independent. So, for the net force to be zero, all the components of the net force should be zero. Therefore, the first condition can be written as
$\sum{F_x}=0$; $\sum{F_y}=0$ and $\sum{F_z}=0$.
i.e., the sum of the forces along the $x$, $y$ and the $z$ axes are separately zero. In static equilibrium, we will focus only on 2-D problems, so we will ignore the $z$-component of the forces.
Condition 2: Net torque is zero:
$\sum{\tau}=0$
Problems solving in static equilibrium
Depends on the problem, sometimes you will only need the first condition or only the second condition to solve the problem. But in most cases, you may need to use both the conditions to solve problems.In the first condition, you need to add all the forces acting on the object along the $x$-axis and set that equal to zero. Likewise, add all the forces acting along the $y$-axis and set that equal to zero. Then, solve the equations to find the unknowns. If the first condition is not enough to solve the problem, then you need to use the second condition too.
In the second condition, you need to find the torque by all the forces on the object first. Then, add all the torques and set the sum equal to zero. To find the torque, you need a pivot. Choose the pivot such that it passes through the point where an unknown force is acting on the object. This will eliminate that force from the resulting equation.
Elasticity
If a force is applied on an object, the force deforms the object. No matter how small the applied force is, all objects undergo deformation. The amount of deformation depends on three factors: the magnitude of the force, the size of the object and the type of the material of the object. In most cases, the magnitude of deformation is not big enough to be visible.
In the figure above, a force, $\vec F$ is applied on the top of a column. The force compresses the column. We take the initial length of the column as $\ell_0$, and the final length as $\ell$, which is the length with the force acting on. So, the change in length of the object (the column) is $\Delta \ell =\ell-\ell_0$.
Now, if you remove the force, what happens to the object? When the force is removed, the object can either comeback to the original state or not come to the original state. If the force is not too high, most objects comeback to the original state due to a property called elasticity. If an object can comeback to its original state once the applied force is removed, then we say that the force is within a limit called elastic limit.
Stress in an object
A force applied on an object creates a stress within the object. Stress is defined as force per unit area:$stress=\dfrac{F}{A}$
where $A$ is the area over which a force $F$ is applied on the object. If you stretch a wire or compress a column by applying a force, then $A$ is the area of cross section of the wire or the column.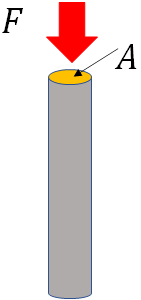
Types of stress
There are three types of stress depends on what the applied force does on the object. If the force stretches the object, then the stress is called tensile stress. If the force compresses the object, the stress is compressive stress and if the force shear the object, it is shear stress.Linear strain or strain
When you apply a force to stretch a wire or compress a column, the length of the object changes. The ratio of the change in length to the original length of the object is called linear strain or just strain.$strain=\dfrac{\Delta l}{l_0}$
where $l_0$ is the original length and $\Delta l$ is the change in length of the object due to the application of the force.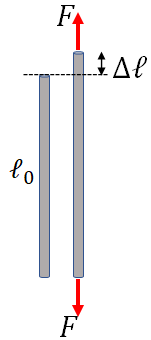
Young's modulus of elasticity
When the applied force is within the elastic limit, the ratio of the stress to the linear strain is constant for a given material of the object. The ratio is called the Young's modulus of the material of the object:$E=\dfrac{stress}{strain}$
Substituting the $stress$ and the $strain$ from the previous equations, we get
$E=\dfrac{F.l_0}{A \Delta l}$Young's modulus is a material property. Different materials have different values of Young's modulus. It is independent of the object's length or width.
Shear strain, shear stress, and the shear modulus of elasticity
A shearing force applied on a side of an object while the opposite side is fixed, changes the shape of the object. In the following figure, a shearing force is applied on the top side of an object (a cube) as shown, while its bottom side is fixed.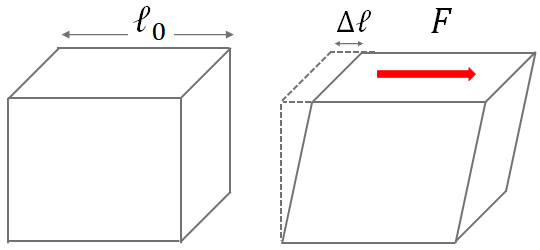
The strain produced by the shearing force is called shear strain, and the stress produced is called shear stress. They are,
$shear \: strain=\dfrac{\Delta l}{l_0}$
and
$shear \: stress=\dfrac{F}{A}$
where $A$ is the area of the side where the force is being applied.It is found that the ratio of the shear stress to the shear strain is constant for a given material of the object. The constant is called shear modulus, $G$:
$G=\dfrac{shear\:stress}{shear\:strain}$
Substituting for $shear \: stress$ and $shear \: strain$ from the previous equations, we get,
$G=\dfrac{F.l_0}{A \Delta l}$Volume strain, pressure change and the bulk modulus of elasticity
When an object is submerged in a fluid, the fluid pressure exerts forces on the surface of the object. As a result, the object is compressed and its volume changes.The ratio of the change in volume to the original volume of the object is called, volume strain:
$volume \:strain=\dfrac{\Delta V}{V_0}$
where $V_0$ is the original volume of the object and $\Delta V$ is the change in volume due to the pressure change.
The ratio of the change in pressure to the volume strain is constant for a given material of the object. The ratio is called bulk modulus, $B$:
$B=\dfrac{change\:in\:pressure}{volume \: strain}$
(or)$B=-\dfrac{V_0.\Delta P}{\Delta V}$
where $\Delta P$ is the pressure change the object undergoes.A minus sign is included in the above equation to make $B$ positive as when the pressure increases (positive $\Delta P$) volume decreases ($\Delta V$ is negative).
Note that all the three moduli of elasticity: $E$, $G$ and $B$ are the properties of materials. They are independent of the size or shape of the objects.
