Two dimensional motion
You studied one dimensional (1-D) motion, in which an object moves on a straight path. In a two or three dimensional motion, an object moves on a non straight path. If the path can be put on a plane, then it is two dimensional (2-D), otherwise it is three dimensional (3-D). In a 1-D motion, we need only one variable, $x$ or $y$ to represent the position of the object. But we need two variables to represent the position of an object in a 2-D motion. An example for a 2-D motion is a projectile motion. In this page, you will learn about projectile motion, and relative velocity in 2 dimensions.Projectile motion
The motion of a launched object into the air, which is only under the influence of gravity is called projectile motion. And, the launched object is called a projectile. You know that any object moving in air has air resistance acting on. But we ignore the air resistance as it is not significant in most cases. The 1-D free fall motion that you learned before is also a projectile motion, but that is a 1-D projectile motion. Now, you are going to learn about 2-D projectile motion. To separate the 2-D projectile motion from the 1-D free fall motion, we use the term projectile only for the 2-D motion. So, the projectile motion is the motion of an object in air that is launched either horizontally or at an angle from the horizontal. Thus, we exclude the vertically launched or dropped object from projectiles as they are 1-D free fall motion.In the animation below, a ball moves on a surface initially. Then it leaves the surface.When the ball is on the surface it is under the influence of the surface. But once it leaves the surface, it comes only under the influence of gravity, ignoring the air resistance. So, the ball becomes a projectile as soon as it leaves the surface. Since the direction of velocity when the ball becomes a projectile is horizontal, this projectile is launched horizontally.
In the following animation, you see that the projectile (the cannon ball) is launched at an angle from the horizontal.
Whether a projectile is launched horizontally or at an angle from the horizontal, the path of a projectile is a parabola. We can draw the path of a projectile with the equation of a parabola.
Breaking the 2-D projectile motion into two 1-D motions
The animation below shows the motion of a projectile (the ball) that is launched (thrown) into the air at an angle from the horizontal. To describe the projectile motion, we put the frame of reference such that the $x$- axis in the horizontal direction (parallel to the Earth's surface) and the $y$ - axis in the vertical direction (perpendicular to the Earth's surface).
In the animation, the black arrow represents the velocity vector of the projectile. The length of the arrow is the magnitude of the velocity, which is the speed of the projectile and the arrowhead shows the direction of the velocity. You can see that both the magnitude and direction of the velocity changes continuously. First, the projectile moves upward, until it reaches the highest point, and then it moves downward. When the projectile moves upward, its speed decreases until it reaches the highest point, where the speed is minimum. After the highest point, the speed of the projectile increases as it move downwards until it hits the ground.
Galileo studied the projectile motion in the 17th century. He showed that a projectile motion can be studied by considering the horizontal and the vertical motion separate. In the animation below, the blue circle represents the horizontal motion of the projectile and the green circle, its vertical motion. According to Galileo, horizontal and the vertical motion of a projectile are independent. That is, the motion of the blue ball does not affect the motion of the green ball and vice versa. So, to study the 2-D projectile motion, we just need to study two 1-D motions, the horizontal motion and the vertical motion separately. And, for each 1-D motion, we can use the 1-D kinematic equations.
Since we take the horizontal motion along the $x$ axis, and the vertical motion along the $y$ axis, the horizontal displacement of the projectile is $\Delta x$ and the vertical displacement is $\Delta y$. We take, $v_x$ and $a_x$ are the horizontal velocity and the horizontal acceleration of the projectile. And, $v_y$ and $a_y$ are the vertical velocity and vertical acceleration of the projectile. Note that the velocity and acceleration are vectors. So, $v_x$ and $v_y$ are the $x$ and the $y$ components of the velocity vector. And, $a_x$ and $a_y$ are the $x$ and the $y$ components of the acceleration vector.
Since the horizontal and the vertical motion are independent, only the $x$ components of displacement, velocity and acceleration are related to each other. Likewise, only the $y$ components are related to each other.
To obtain the equations describing a projectile motion, we start with the acceleration of the projectile.
Horizontal and vertical acceleration of a projectile
The acceleration of a projectile is the result of gravity. The gravity is a pull (or a force) that acts vertically downward only. So, the gravity can affect only the vertical motion, and it has no effect on the horizontal motion. So, the horizontal acceleration of a projectile is zero:i.e., $a_x=0$
Since the gravity acts vertically downward, there is a vertical acceleration, which is the acceleration due to gravity. If we take positive upward, then the vertical acceleration of the projectile is
$a_y=-g$
Initial velocity of a projectile
All projectiles have a launching velocity, called initial velocity. We take the initial velocity as $\vec v_0$. The magnitude of the initial velocity is $v_0$, which is the initial speed of the projectile.For a projectile that is launched at an angle θ above the horizontal, the initial velocity vector, $\vec v_0$ and its components, $v_{0x}$ and $v_{0y}$ are shown in the figure below.
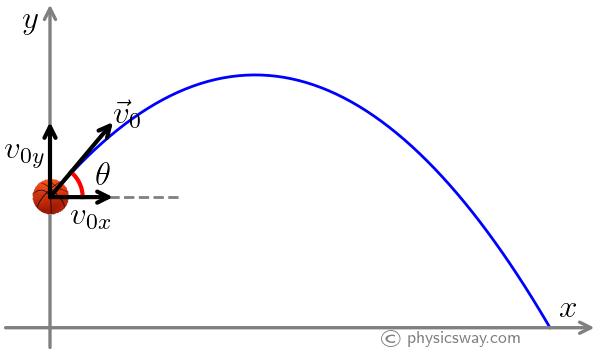
From the figure, the $x$ and the $y$ components of the initial velocity are
$v_{0x}=v_0 \cos\theta$ and $v_{0y}=v_0 \sin\theta$
Note that, $v_{0x}$ is nothing but the initial horizontal velocity and $v_{0y}$ is the initial vertical velocity of the projectile.
For a projectile that is launched horizontally, the initial velocity vector, $\vec v_0$ is in the $+x$ direction as in the figure below.
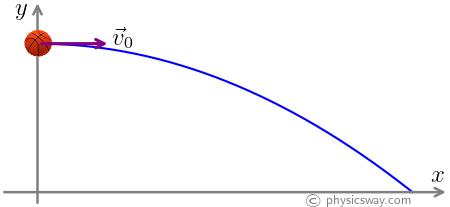
So, for a horizontal launch, the $x$ and the $y$ components of the initial velocity are
$v_{0x}=v_0$ and $v_{0y}=0$.
Note that for a horizontal launch, the vertical velocity is zero.
Now, we have the acceleration and the initial velocity for the the horizontal and the vertical motions. Next, we need the equations for each motion.
Equations for the horizontal motion
Since the horizontal acceleration $(a_x)$ of a projectile is zero, the horizontal velocity is a constant. So, the horizontal velocity, $v_x$ of a projectile at any time is same as its initial horizontal velocity. That is,$\boxed{v_x=v_{0x}}$
We use the 1-D kinematic equation to study the horizontal motion as it is a 1-D motion. If we substitute, acceleration equal to zero in the second or the third kinematic equation, we get the following equation,
$\boxed{\Delta x=v_{0x}t}$
Note that in the kinematic equation(s), I added the subscript $x$ to the initial velocity as we are dealing with the horizontal motion.
Equations for the vertical motion
We saw that the vertical acceleration of a projectile is the acceleration due to gravity. So, the vertical motion of a projectile is exactly the same as the 1-D free fall motion. Thus, we can use the 1-D free fall equations to study the vertical motion. If we take positive upwards, then we have the following equations for the vertical motion of a projectile.$v_y=v_{0y}-gt$
$\Delta y=v_{0y}t-\frac{1}{2}gt^2$
$v_y^2=v_{0y}^2-2g\Delta y$
Note that I have added a subscript $y$ to the velocities in the free fall equations to get the above equations as these equations are for the vertical motion.
You learned in free fall motion that at the highest point the velocity is zero. So, at the highest point, the vertical velocity of a projectile is zero. That is,
$v_y=0$ at the highest point.
Velocity of a projectile If you know the vertical velocity, $v_x$ and the horizontal velocity, $v_y$ of a projectile at any time $t$, then you can find the velocity of the projectile at that time.
The magnitude of velocity (speed) of the projectile at time $t$ is
$v=\sqrt{v_x^2+v_y^2}$.
And the direction of velocity, $\theta$ can be obtained using the equation,
$\tan \theta =\dfrac{v_y}{v_x}$.
Note that this angle, $\theta$ is not same as the initial launching angle. This angle is different at different times as the velocity of the projectile changes continuously.
Velocity at the highest point
If you launch a projectile at an angle above the horizontal, then there is a highest point in the trajectory of the projectile. What is the velocity of the projectile at the highest point? Is it zero?. At the highest point, the vertical velocity, $v_y=0$. But the horizontal velocity, $v_x$ is not zero, because it is a constant, which is always there. So, the velocity of a projectile is not zero at the highest point. You can find the magnitude of the velocity at the highest by substituting, $v_y=0$ in the equation,$v=\sqrt{v_{x}^2+v_y^2}$
$=\sqrt{v_{0x}^2+0^2}$
$=|v_{0x}|$
This is the speed of the projectile at the highest point.
Range of a projectile
The maximum horizontal displacement of the projectile is called the range of the projectile.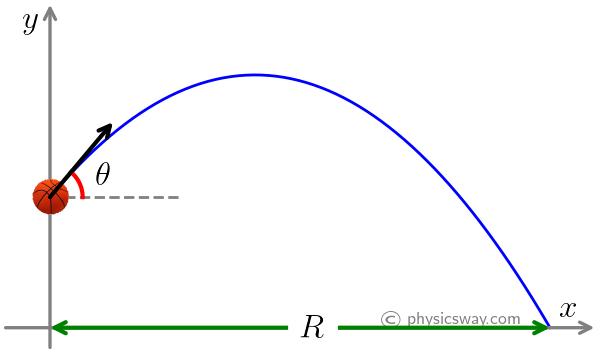
We have, the horizontal displacement of the projectile at time $t$, which is
$\Delta x = v_{0x}t$
If $t$ is the total time of flight, $t_f$, then $\Delta x$ is the range of the projectile. So, the range of a projectile is
$R = v_{0x}\,t_f$
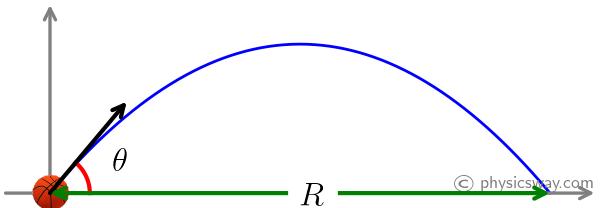
If a projectile is launched from the ground level and landed at the ground, then we can obtain an equation for the range in terms of the initial speed, $v_0$ and the launching angle, $\theta$.
The vertical displacement, $\Delta y=0$ for a projectile that is launched from the ground level and ends at the ground. Substituting, $\Delta y=0$ in the second equation for the vertical motion, and solving for $t$, you get
$t=\dfrac{2v_{0y}}{g}$
This is the total time of flight, $t_f$. Substituting this in the range equation,
$R=\dfrac{2v_{0x} v_{0y}}{g}$
We have, $v_{0x}=v_0 \cos\theta$, and $v_{0y}=v_0 \sin\theta$. Substituting these in the equation, we get
$R=\dfrac{2v_{0}^2 \sin\theta \cos\theta}{g}$
Using the trigonometric identity, $2 \sin\theta \cos\theta = \sin 2\theta$,
$R=\dfrac{v_{0}^2 \sin 2\theta}{g}$
Note that this is valid only if the launching height and the landing height are the same (starting and ending at the ground). According to this equation, for any launching speed, the range will be the same for any two angles, which are complimentary. For example, if you throw a ball from the ground at an angle 30° with some speed, and the range is 100m. Now, if you throw the ball with the same speed at the angle, 60° (which is 90-30 = 60), you will get the same range.
Relative velocity
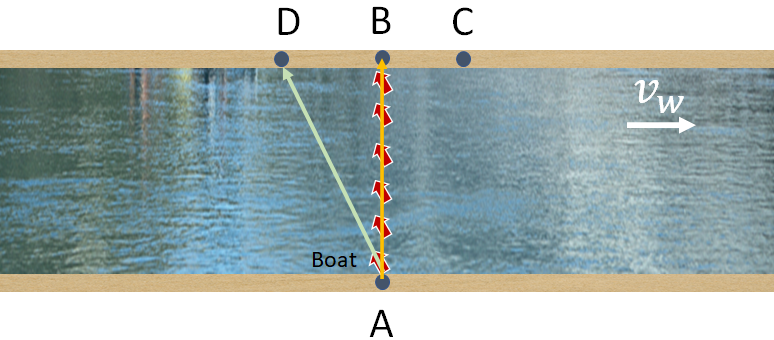
The velocity of an object depends upon the choice of the frame of reference. When a car is moving and you say its velocity is 50 mph, you mean the velocity is relative to the ground, i.e., the frame of reference is fixed somewhere at the ground. Assume you are traveling in a car with a friend. For you, your friend is not moving, but everything outside the car appear to move. So, for you, the velocity of your friend is zero as you measure his/her velocity with respect to a reference frame in the car. But, for a person on the ground, your friend is moving with the car. So, for the person on the ground, the friend's velocity is not zero as he use a different frame of reference, which is the ground. So, velocity is relative: the velocity of an object relative to one reference frame is not the same as the velocity of the same object measured relative to another reference frame.Assume, you are at point A, on the bank of a river with water flowing from west to east. Now, you want to go to the other side of the river in a boat, to a point B that is exactly opposite to what you are now.
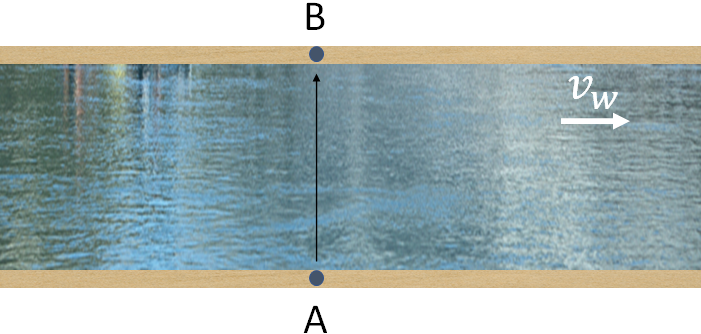
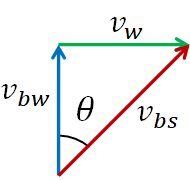
Let the velocity of the water (river) as $v_w$. This is the velocity of the water as observed by a person on the shore (river bank). For the boat, there are two velocities. One is the velocity with respect to the water, $v_{bw}$. This is the velocity of the boat when the water is still, or is the velocity of the boat observed by a person moving with the river. And the other is the velocity with respect to the shore, $v_{bs}$. This is the velocity of the boat as observed by a person on the shore.
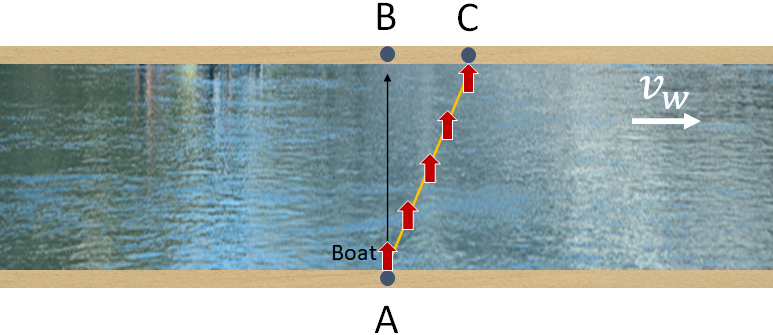
So, the boat has two components of velocities, a vertical component that is $v_{bw}$ and a horizontal component, $v_w$ that results from the water stream. Adding these two velocity vectors, we will get the following right angled triangle.
To find the downstream distance, BC, consider the right angled triangle formed by the points A, B and C.
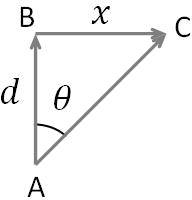
The horizontal downstream distance BC is determined by the horizontal velocity, $v_w$. Therefore,
$x=v_w t$
where $t$ is the time the water takes to move from B to C. This is also the time for the boat to travel to the other side. If the water is still, then the boat takes the same amount of time, $t$ to travel from A to B. So, if d = AB, the width of the river, then
$t=\dfrac{d}{v_{bw}}$
Now, in order to reach the point B, you need to start at a certain upstream angle, i.e., at an angle from the north toward the upstream (west) and with a certain speed. For a correct angle and speed, the boat will have a horizontal velocity component exactly opposite to the velocity of the water stream and cancels each other. So, there will be no horizontal component of the boat velocity, and the boat will travel exactly in the northerly direction to reach the point B.
Putting together all the velocity vectors, we will get the following triangle.
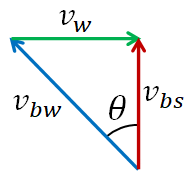
If $d$ is the width of the river, then the time to reach the other side of the river is
$t=\dfrac{d}{v_{bs}}$
Note that, I used the velocity $v_{bs}$ as it is the velocity component along the river width.
