Derivation of work energy principle

i.e.,  $W_{net}=\Delta KE$.

To derive this equation, let us consider an object in 1-D motion with some velocity, $v_i$. Assume the net force on the object is zero.

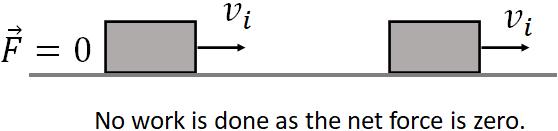
Now, let us apply a constant force, $\vec F$ on the object in the direction of motion for a period of time. At the end of the time period, let the object's velocity is $v_f$ and the object makes a displacement of $d$. $\vec F$ is now the net force acting on the object as the net force was zero before it.

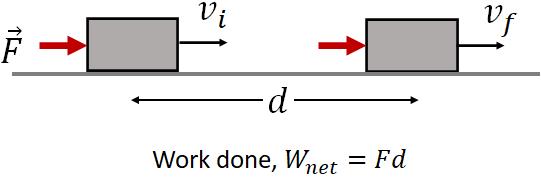
The force does a work on the object. Since $F$ is the net force, a net work is done on the object by the force, which is

$W_{net}=Fd\cos \theta=Fd\cos0=Fd$

The angle, $\theta =0$ as the force and the displacement are in the same direction.

Now, from Newton's second law, we have

$F=ma$

where $a$ is the acceleration of the object and $m$ is its mass.

Substituting this $F$, in the net work equation,

$W_{net}=mad$.

Now, from the fourth kinematic equation, we can write the equation for the final velocity, $v_f$,

$v_f^2=v_i^2+2ad$.

Solving for $a$,

$a=\dfrac{v_f^2-v_i^2}{2d}$

Substituting this $a$ in the work equation above, we get,

$W_{net}=m\bigg(\dfrac{v_f^2-v_i^2}{2d}\bigg)d$.

After canceling $d$ and removing the parenthesis,

$W_{net}=\dfrac{1}{2}mv_f^2-\dfrac{1}{2}mv_i^2$.

Right hand side is the final kinetic energy minus initial kinetic energy, which is just the change in kinetic energy of the object. i.e.,

$W_{net}=\Delta KE$

This is the work-energy principle.

Note that, for simplicity, we assumed that motion is 1-D and the force is constant. But we can derive the equation for any case and the work-energy principle is valid for any situation.