Circular motion
If an object moves on a circular path, then the motion of the object is called circular motion. A ball at the end of a string that swing in a circle, motion of the Moon around the Earth are some examples of circular motion.In this page, you will learn about the following, uniform circular motion, banked and unbanked highway curves or roads, law of universal gravitation, acceleration due to gravity on any planet, and the Kepler's laws.
Velocity of an object in a circular motion
In the animation below, you can see that an object is in circular motion. The red arrow is the velocity vector of the object. The direction of velocity of the object changes continuously. And, at any instant of time, the direction of velocity is tangent to the circle.Uniform circular motion
If the speed of an object in a circular motion is constant, we call that a uniform circular motion. Although speed is constant, the velocity of an object in uniform circular motion is not constant as the direction of velocity is not constant. So, an object in uniform circular motion has an acceleration.Centripetal force
According to Newton's first law, an object in motion will continue its motion on a straight line as long as there is no net external force acting on it. Circular motion is not a motion on a straight line path. So, there must be a net external force acting on the object to keep it on the circular path. That net external force, we call, the centripetal force, $\vec F_c$.When a ball attached with a string swing in a circle, the string pulls the ball towards the center of the circle. So, the string exerts a force on the ball towards the center. The force, the string exerts on the ball is the force of tension. This force of tension is what keep the ball in circular motion. So, here the centripetal force is the force of tension.
The Moon revolves around the Earth on a nearly circular orbit. The force of gravity on the Moon by the Earth keeps the moon in its orbit around the Earth. So, the force of gravity is the centripetal force here. The force of gravity is toward the center of the Earth, which is the center of the circle. So, the centripetal force is towards the center of the circle. Thus, the the direction of the centripetal force on any object in circular motion is toward the center of the circle.
Acceleration in uniform circular motion
The acceleration of an object in a uniform circular motion is called the centripetal acceleration, $\vec a_c$. This centripetal acceleration is due to the centripetal force on the object. So, the direction of the centripetal acceleration is also towards the center of the circle at any instant of time.If an object is in uniform circular motion on a circle of radius $r$, with speed $v$, then the magnitude of the centripetal acceleration of the object is
$a_c=\dfrac{v^2}{r}$
The derivation of this equation is given in this page, deriving centripetal acceleration.
Magnitude of the centripetal force The centripetal force is related to the centripetal acceleration by Newton's second law,
$\vec F_c=m\, \vec a_c$
where $m$ is the mass of the object.
So, the magnitude of the centripetal force is
$F_c=ma_c=\dfrac{mv^2}{r}$
Period of circular motion
If an object continues the motion on a circle, it repeats the motion in a certain time interval. The time interval is the period of the circular motion. So, period, $T$ is the time taken by the object to complete one circle. In a time, $T$, the object travels a distance equal to the circumference of the circle, which is $2\pi r$. From the distance and the time, we can find the speed of the object,$v=\dfrac{2\pi r}{T}$
Solving for $T$, we will get the period,
$T=\dfrac{2\pi r}{v}$
Unbanked and banked high way curves
There are two types of highway curves (or roads), unbanked and banked curves. Banked curve is advantageous during the snowy season as it provides better control against vehicles slide off when making a turn.
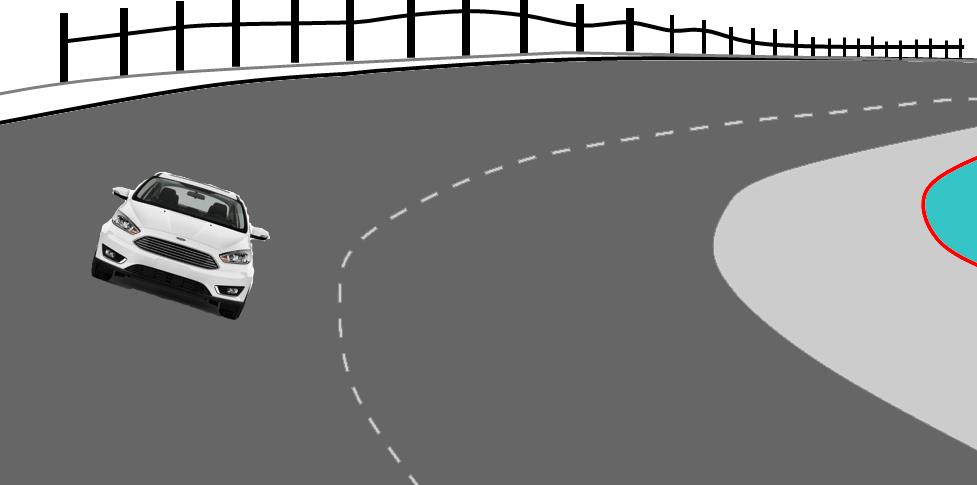
Unbanked curve
The unbanked roads are horizontal or flat roads. When a car or a truck travels on an unbanked curve, it is in circular motion. If a flat road is icy and has no friction, then a car cannot follow a curve on the road. So, on an unbanked road, friction is required to follow a curve. Thus, on an unbanked curve, friction is the centripetal force. So, the centripetal force on the vehicle is$F_c=F_{fr}$
where $F_{fr}$ is the force of friction between the road and the tires of the vehicle.
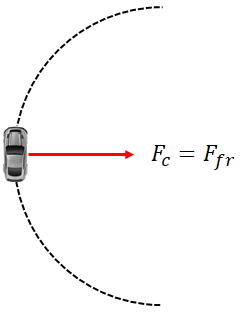
Now, the question is what type of friction provides the centripetal force to a vehicle on an unbanked flat road? is it static or kinetic ? Since friction is the centripetal force on a horizontal curve, its direction should be towards the center of the circle. But there is no motion of the vehicle in that direction, so the friction is static.
Depends upon the friction between the road and the tires, there is a maximum speed, above which a car cannot follow a curve or make a turn on a flat road. This maximum speed,$v_{max}$ can be obtained by equating centripetal force to the maximum available force of friction:
$\dfrac{mv_{max}^2}{r}=\mu_sF_n$.
If $m$ is the mass of the vehicle, then the normal force on the car, is $F_n=mg$. Substituting this in the above equation, and solving for $v_{max}$, we get,
$v_{max}=\sqrt{\mu_s rg}$This is the maximum speed at which a car can safely follow a horizontal curve. If there is ice on the road, then $\mu_s$, decreases that reduces the safe speed. Note that the maximum speed is independent of the mass of the vehicle.
Banked curve
A banked curve is tilted above the horizontal by an angle, usually toward the inside of the curve. The angle of the tilt is called the banking angle. The path of a banked curve is actually a part of a horizontal circle as shown in the figure below. For a car or a truck to follow the curve, there must be a horizontal force acting on it toward the center of the circle, which is the centripetal force.How can we have a horizontal force on the car so that it can follow the curve?. If you look at the normal force on the car, it is not vertical. That means, there is a horizontal component of the normal force towards the center of the circle. This component of the normal force acts as the required centripetal force for the car to follow the curve.
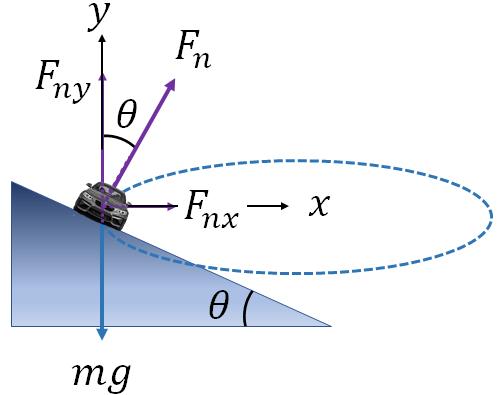
Let us take the $x$ axis towards the center of the circle and the $y$ axis vertical. From the geometry of the figure, you can see that the normal force is at an angle $\theta$ from the vertical. Finding the $x$ and the $y$ components of the normal force, we have
$F_{nx}=F_n \sin\theta$ and
$F_{ny}=F_n \cos\theta$
Since the $x$ component of the normal force is the centripetal force, we can write
$F_n \sin\theta=\dfrac{mv^2}{r}$
From the figure, normal force does not balance the force of gravity, $mg$, but the $y$ component of the normal force does. Therefore,
$F_n \cos\theta=mg$.
Dividing the previous equation by this equation, we get,
$\tan \theta = \dfrac{v^2}{rg}$
Solving for $v$,
$v=\sqrt{rg\tan\theta}$
This $v$ is called the design speed or the safe speed to drive on a banked curve. The design speed is independent of the mass of the vehicle.Note that, when deriving the above equation we ignore the friction force on the tires by the road. So, a car can follow a banked curve even without friction.
Law of universal gravitation
The law of universal gravitation was published by Isaac Newton in 1687. It states that"every particle in the universe attracts every other particle with a force, which is proportional to the product of their masses and inversely proportional to the square of the distance between them."
If there are two objects, they attract each other with a force called gravitational force. The magnitude of the gravitational force between any two objects is given by
$F_g=G\dfrac{m_1m_2}{r^2}$
where $m_1$ and $m_2$ are the masses of the objects; $r$ is the distance between the objects that it is measured from the center to center of the objects; and $G$ is a constant, called, the gravitational constant. The value of $G$ is$G=6.67\times10^{-11}Nm^2/kg^2$.
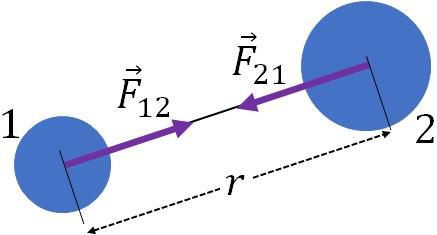
In the figure, you see that, object 1 exerts a gravitational force, $\vec F_{21}$ on object 2 towards it and the object 2 exerts a gravitational force, $\vec F_{12}$ on object 1 towards it. These two forces are equal and opposite, according to Newton's third law. The magnitudes of the forces are given by the law of gravitation. That is
$|\vec F_{12}|=|\vec F_{21}|=F_g$
Acceleration due to gravity on or near a planet
You already learned that near the surface of the Earth, acceleration due to gravity, $g$ is $9.80 m/s^2$. This is valid only near the surface of the Earth. Acceleration due to gravity decreases with altitude.Now, we are going to derive an equation for acceleration due to gravity near a planet or a celestial object. Let $M_p$ is the mass of the planet or the celestial object. Assume that you want to find the acceleration due to gravity at a point P, which is at a distance $r$ from the center of the planet. Imagine that there is a test object of mass, $m$ at P.
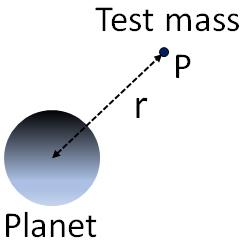
Let $g$ is the acceleration due to gravity of the object at the point P. So, the force of gravity on the test object is
$F_g=mg$
Force of gravity is actually the gravitational force on the object by the planet that you can also find by using the law of universal gravitation,
$F_g=G\dfrac{mM_p}{r^2}$.
Now, equate the two equations above and solve for $g$, you will get,$g=\dfrac{GM_p}{r^2}$.
Acceleration due to gravity depends on the planet's mass and the distance from its center. It decreases with distance as $1/r^2$, an inverse square law.
On the surface of the Moon, the acceleration due to gravity, $g$ is about one-sixth of that on the Earth, because of its smaller mass.
Satellites
Satellites revolve around the Earth in nearly circular orbits. Man made satellites are used for various applications from weather forecasting to navigation. Since a satellite is in circular motion, there must be a centripetal force acting on the satellite. That centripetal force is actually the gravitational force on the satellite by the Earth.If $m$ is the mass of a satellite that is revolving around the Earth, then the gravitational force on the satellite by the Earth is
$F_g=G\dfrac{M_E\,m}{r^2}$.
where $M_E$ is the mass of the Earth and $r$ is the radius of the orbit, which is the distance of the satellite from the center of the Earth.
Since the gravitational force is the centripetal force, we have
$\dfrac{mv^2}{r}=G\dfrac{M_E\,m}{r^2}$.
Solving for $v$,we get,
$v=\sqrt{\dfrac{GM_E}{r}}$.In the above equation, there is no $m$, the mass of the satellite, so the speed of a satellite is independent of its mass. Speed depends only on the distance $r$. It varies as $1/\sqrt{r}$. So, closer the satellite to the Earth, faster it moves.
Geosynchronous satellites
Satellites that appear to stay at the same spot above the Earth are called a geosynchronous satellites. For a satellite to be geosynchronous, it should meet two conditions: (i) the orbital period of the satellite should be same as the Earth's rotational period, and (ii) the orbit should be exactly aligned with the equator of the earth. So, the period of a geosynchronous satellite is 1 day, the earth's rotational period. Since a geosynchronous satellite appears to be fixed at one spot above the Earth, they are used for satellite television broadcasts and communication purposes. Based on the period, we can estimate that a geosynchronous satellite orbits the Earth at a height of approximately 36,000 km with a speed of about 2800 km/h.Weightlessness
We all feel weight due to a normal force acting on us. When there is no normal force, we feel weightlessness. You can realize this by standing in an elevator. When the elevator accelerates downward, you feel less weight, and when it accelerates upward you feel more. The weight that you feel is the normal force (also called apparent weight) exerted on you by the surface of the elevator. As you already learned in "forces", the normal force on a person in an elevator is$F_{n}=mg+ma$
where $a$ is the acceleration of the elevator (or the person).If the elevator cable suddenly breaks, then the elevator and the person are in free fall. Since the person is in free fall, her/his acceleration, is $a=-g$. If you substitute this in the above equation, you get $F_{n}=0$, and the person feels weightlessness. An astronomer in a spacecraft is also in free fall along with the spacecraft as gravity is the only force acting on the astronomer or the spacecraft, so he/she feels weightlessness. Note that one feels weightless due to the absence of normal force. Although apparent weight is zero during free fall, the actual weight of the person is not zero, which is still $mg$.
Planetary motion
All the planets including Earth revolve around the sun. There are three laws developed by Johannes Kepler (1571 - 1630) to describe the motion of planets around the Sun. These laws were developed in the 1600’s, even before the invention of the telescope and also about 50 years before the Newton’s laws.Kepler’s first law:
Each planet revolves around the Sun in an elliptical path with the Sun at one focus.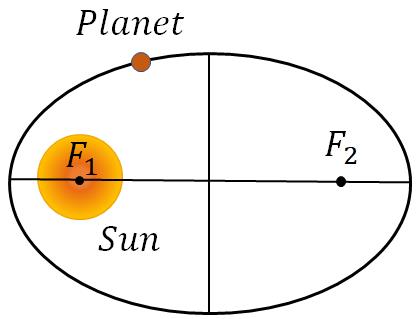
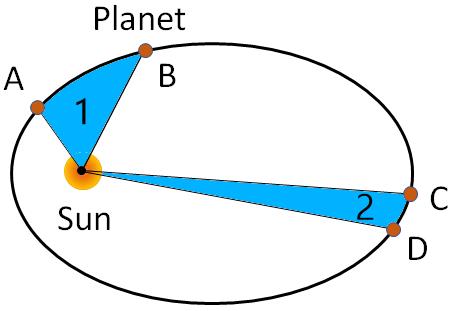
Kepler’s second law:
An imaginary line drawn from the Sun to a planet sweeps out equal areas in equal times.In the figure, the shaded areas 1 and 2, are the same if the time taken by the planet to move from A to B is same as that from C to D.
Kepler’s third law:
The ratio of the squares of the periods of any two planets revolving around the Sun is equal to the ratio of the cubes of their mean distances from the Sun.$\bigg(\dfrac{T_1}{T_2}\bigg)^2=\bigg(\dfrac{s_1}{s_2}\bigg)^3$
where $T_1$ and $T_2$ are the periods of planets 1 and 2 and $s_1$ and $s_2$ are their distances from the sun. For circular orbits, $s=r$, the radius of the orbit.