Derivation of the centripetal acceleration
To derive the centripetal acceleration of an object in uniform circular motion, we consider an object moving on a circle of radius $r$. Let $v$ is the speed of the object, which is a constant.
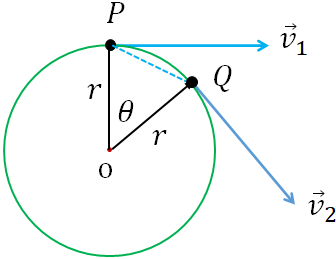
Now, let us take two points on the circle, P and Q separated by an angle $\theta$ as in the figure above. Let $\Delta t$ is the time the object takes to move from P to Q. The velocity of the object is tangent to the circle at any moment of time. So, at the points, P and Q, the velocity vectors are as shown. Let us take, $\vec v_1$ is the velocity of the object at the point P and $\vec v_2$ is the velocity at the point Q.
Next, move the vector $\vec v_2$ and connect its tail with the tail of the vector $\vec v_1$. From the geometry of the first figure, you get the angle between the two vectors as $\theta$. Now, draw a vector (the red arrow) from the tip of the vector, $\vec v_1$ to the tip of the vector, $\vec v_2$.
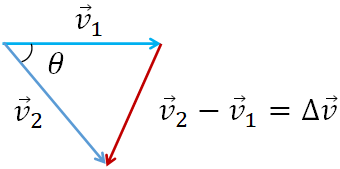
According to the tip-to-tail method, the vector representing the red arrow is $\vec v_2-\vec v_1$, which is the change in velocity $\Delta \vec v$.
Since the speed is constant, $|\vec v_1|=v$ and $|\vec v_2|=v$. So, considering only the magnitudes of the vectors, we get the following triangle,
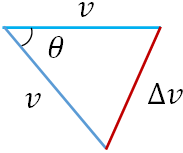
From the first figure, we have another triangle,
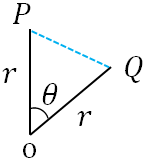
The above two triangles are similar triangles. So, the ratio of the corresponding sides should be the same. Therefore, we can write
$\dfrac{\Delta v}{PQ}=\dfrac{v}{r}$
Solving for $v$,
$\Delta v=\dfrac{v\,PQ}{r}$
Dividing by $\Delta t$, we get
$\dfrac{\Delta v}{\Delta t}=\dfrac{v}{r}\dfrac{PQ}{\Delta t}$
The left hand side is the average acceleration, $\bar a$, and PQ is the displacement of the object in a time, $\Delta t$. So, $\dfrac{PQ}{\Delta t}$ is the average velocity, $\bar v$ of the object. Substituting these, we get
$\bar a =\dfrac{v}{r}\,\bar v$
This is the average acceleration of the object over the time interval, $\Delta t$. We are interested in the instantaneous acceleration. To get the instantaneous acceleration, we just need to take a small time interval because when $\Delta t$ is small, the average values become instantaneous values.
i.e., when $\Delta t \rightarrow\:0$, $\bar a =a$ and $\bar v =v$. And we get,
$a=\dfrac{v}{r}\,v$
$=\dfrac{v^2}{r}$
This is the centripetal acceleration.
