Elastic collisions

In an elastic collision, momentum and kinetic energy, both are conserved. Collision between hard objects is generally elastic. Some of the examples of elastic collision are collision between billiard balls, collision between atoms or molecules. During an elastic collision, no heat or other energy is produced, so there is no loss in kinetic energy.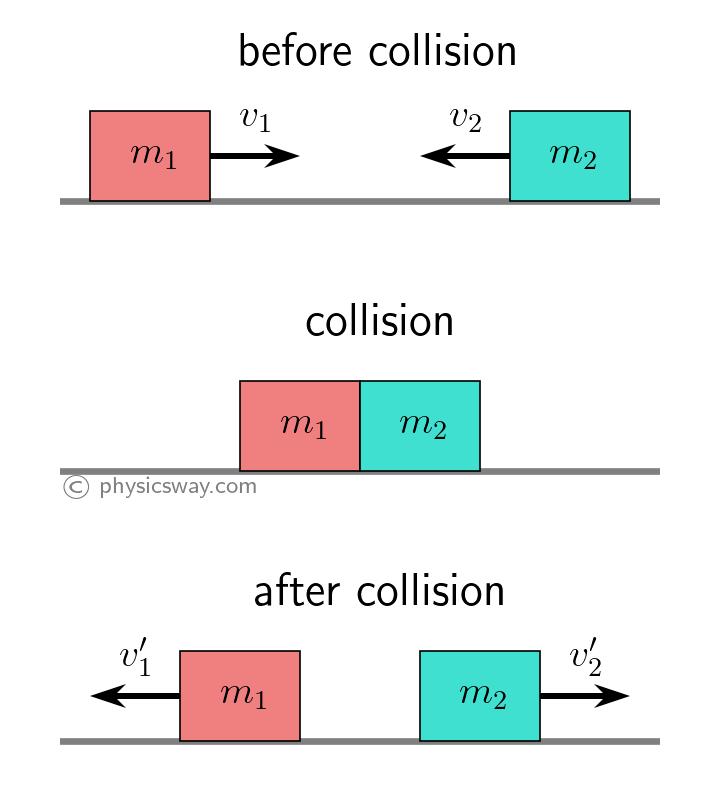

The figure above shows two objects in an elastic collision. The mass of object 1 is $m_1$ and that of object 2 is $m_2$. The velocities of the objects before and after the collision are shown in the figure.

When objects involve in a 1-D elastic collision, we have two equations to solve, one is the law of conservation of momentum and the other is for the conservation of kinetic energy:

$m_1v_1+m_2v_2=m_1v_1'+m_2v_2'$. (1)

and

$\dfrac{1}{2}m_1v_1^2+\dfrac{1}{2}m_2v_2^2=\dfrac{1}{2}m_1v_1'^2+\dfrac{1}{2}m_2v_2'^2$ (2)

The left hand side is the total kinetic energy of the objects before the collision and the right hand side is that after the collision.

To solve problems that involve elastic collision, you need to use these two equations. But solving these two equations are time consuming. The good thing is we can arrive another simple equation from the above two equations as follows.

Take the equation (1) and rearrange so that all the $m_1$ terms are on the left hand side and the $m_2$ terms are on the right hand side. Then, factor out $m_1$ in the left hand side and factor out $-m_2$ in the right hand side:

$m_1(v_1-v_1')=-m_2(v_2-v_2')$. (3)

Next, take the equation (2), divide out the $\dfrac{1}{2}$. Then, rearrange as we did for equation (1) that the $m_1$ terms are on the left hand side and the $m_2$ terms are on the right hand side. And, factor out $m_1$ in the left hand side and factor out $-m_2$ in the right hand side:

$m_1(v_1^2-v_1'^2)=-m_2(v_2^2-v_2'^2)$. (4)

Dividing equation (4) by (3),

$\dfrac{v_1^2-v_1'^2}{v_1-v_1'}=\dfrac{v_2^2-v_2'^2}{v_2-v_2'}$

Using the difference of squares formula, $a^2-b^2=(a+b)(a-b)$, we can write,

$\dfrac{(v_1+v_1')(v_1-v_1')}{v_1-v_1'}=\dfrac{(v_2+v_2')(v_2-v_2')}{v_2-v_2'}$

There are factors you can cancel out. After canceling,

$v_1+v_1'=v_2+v_2'$

Next, rearrange the terms such that all the velocities before the collision on the left hand side and the velocities after the collision on the right hand side. And factor out a negative sign on the right hand side, you will get,

$\boxed{v_1-v_2=-(v'_1-v'_2)}$ (5)

This equation is simpler than equation (2). So, instead of using equations (1) and (2), we can use equations (1) and (5) to solve problems involving elastic collision.