Sound
Sound is a vibration that propagates as a wave through material media such as air, liquids and solids. Sound waves can be produced by vibrating strings, vibrating membranes, vibrating metals, and vibrating air columns.Characteristics of Sound
Sound can travel through any kind of matter, but not through a vacuum. In gases and liquids sound transmits as longitudinal waves. Speed of sound is different in different materials: it is slowest in gases, faster in liquids, and fastest in solids. When sound waves propagate it makes particles in the medium oscillate but it does not carry with them.Speed of sound in air
In air, speed of sound varies with temperature. Sound speed, $v$ increases with air temperature as$v=331+0.60\,T$
where $T$ is the temperature in $^\circ C$ and $v$ is in $m/s$.Intensity and loudness
Energy of a sound wave is proportional to the square of the amplitude of the wave:$E\propto A^2$
Power of the sound wave is the energy a wave transports per unit time:
$P=\dfrac{E}{t}$
where E is the amount of energy the sound wave transmits in a time $t$.
Intensity of a sound wave is the energy it transports across unit area per unit time. Since power is energy per unit time, intensity is the power per unit area.
Loudness of sound is related to the intensity, higher the intensity, louder the sound. Human ear can detect sounds with an intensity as low as $10^{-12}\:W/m^2$. This intensity is called the threshold intensity of hearing.Audible range
Pitch is the frequency of sound. Human ears can hear only the sound with frequencies in the range $20 Hz$ to $20kHz$. This is called the audible range.Perceived loudness and decibels
Although the loudness depends on the intensity of the sound, perceived loudness is not linearly proportional to the intensity, but it is closely related to the logarithm of the intensity. So a logarithmic scale is commonly used for sound level with unit of decibels (dB). Sound level in decibels $(dB)$ is defined as$\,\beta=10\,\log\left( \dfrac{I}{I_0}\right)$
where $I$ is the intensity of the sound and $I_0$ is the threshold intensity of hearing. i.e., $I_0=10^{-12}\:W/m^2$Sound intensity versus distance
Intensity of sound diminishes with distance. If you move away from the source, the sound intensity decreases with distance as an inverse square law,$I=\dfrac{P}{4\pi r^2}$
where $P$ is the power output of the sound source and $r$ is the distance from the source.
Proof of this equation is as follows.
Consider a source of sound that send out sound waves uniformly in all directions. To find the intensity at a point A, which is at a distance $r$ from the source, form a sphere of radius $r$ with the source at the center.
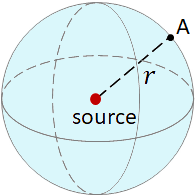
All the sound waves coming from the source pass through the surface of the sphere. So, the intensity of the sound wave on the surface is
$I = \dfrac{P}{A}$
where $A$ is the surface area of the sphere, $A=4\pi r^2$.
Therefore,
$I=\dfrac{P}{4\pi r^2}$
Sources of Sound
Stringed instruments such as guitars produce sound waves by vibrating plucked strings and wind instruments such as flutes produce sound by blowing and subsequent vibration of the air column within the instruments.Vibrating string resonance
A plucked string in a musical instrument can vibrate only at certain frequencies, called the resonant frequencies of the string. These frequencies are the frequencies of the standing waves on the string. So, a stringed instrument can produce sound of frequencies at the resonant frequencies of the string.Resonant wavelengths on a stretched string are
$\lambda_n=\dfrac{2\ell}{n}$ where $n=1,2,3 ...$
andResonant frequencies are
$f_n=n \dfrac{v}{2\ell}$ where $n=1,2,3, ...$
The frequency corresponds to $n=1$, i.e., $f_1=\dfrac{v}{2l}$ is called the fundamental frequency. All other frequencies (except the fundamental) are called overtones. All resonant frequencies corresponds to $n=1,2,3, ...$, i.e., $f_1,f_2,f_3, ...$ are called are called harmonics.Wind instruments
A wind instrument create sound through standing waves in a column of air. A wind instrument can be a closed tube, a tube closed at one end or an open tube, a tube open at both ends.Closed tube resonance
In a tube closed at one end, the air molecules cannot vibrate at the closed end. This restriction limits the possible resonant frequencies of the tube. The first three possible standing waves in a closed tube are as follows: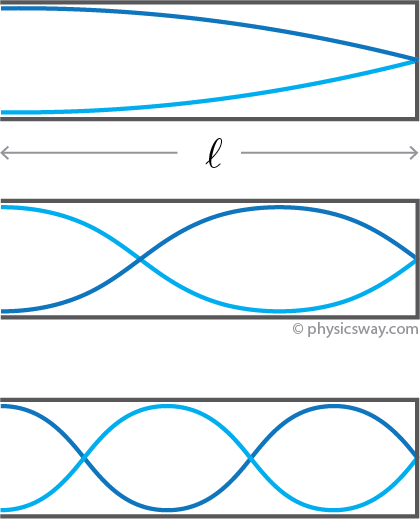
For the standing wave in the first figure, there is a quarter of the wave over the length of the tube, $\ell$ therefore,
$\ell=\lambda_1/4$
or$\lambda_1= 4\ell$
In the second figure, there is a 3/4 th of the wave in the tube therefore,
$\ell=3\,\lambda_2/4$
or$\lambda_2= 4\ell/3$
In the third figure, there are 1 and a quarter wave, therefore,
$\ell=5\,\lambda_3/4$
or$\lambda_3= 4\ell/5$
Like these there are infinite number of possible resonant wavelengths. If we combine those equations, we will end up with an equation:$\lambda_n=\dfrac{4\ell}{n}$, where $n=1,3, 5,7,...$
By using $v=f\lambda$, we can write the resonant frequencies of the closed tube:
$f_n=n\dfrac{v}{4\ell}$, where $n=1,3,5,7, ...$
The frequency corresponds to $n=1$ is the fundamental frequency. All resonant frequencies are called harmonics. Frequencies other than the fundamental are called overtones.
Open tube resonance
In a tube open at both ends, when blown, the air molecules always vibrate with higher amplitudes at the end of the tubes. Due to this, the resonant frequencies of the tube are restricted to certain frequencies. The first three possible standing waves in a open tube are given below.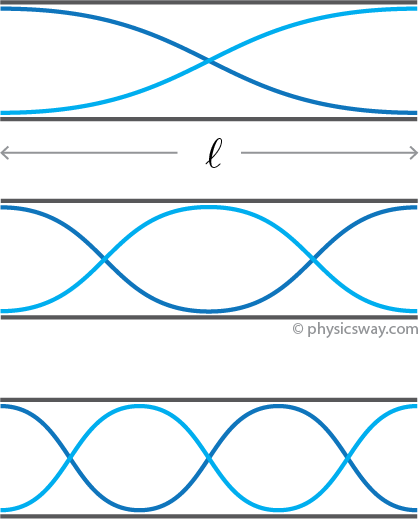
Taking the standing wave in the first figure, there is a half wave over the length of the tube, so we have
$\ell=\lambda_1/2$
or$\lambda_1= 2\ell$
In the second figure, there is a full wave over the tube's length, so we have$\ell=\lambda_2$
or$\lambda_2= \ell$
In the figure three, there are 1 and a half wave, and therefore$\ell=3\,\lambda_3/2$
or$\lambda_3= 2\,\ell/3$
Combining the above equations, we can write,$\lambda_n=\dfrac{2\ell}{n}$, where $n=1,3, 4,...$
These are the resonant wavelengths of an open tube. From this equation, we can write the resonant frequencies,$f_n=n\dfrac{v}{2\ell}$, where $n=1,2,3,...$
Doppler Effect
When a source of sound is moving toward a stationary observer, the pitch of sound the observer hears is higher than that when the source is at rest. And, when the source is moving away from the observer, the pitch is lower. This phenomenon is called Doppler effect. You can experience Doppler effect with the siren of a fire truck, a police car or an ambulance. When a fire truck approaches you, you hear the pitch of its siren increases and as it passes by and move away from you, you hear the decrease in pitch.Doppler effect depends on the velocity of the source, the velocity of the observer (if the observer is moving) and the direction of their motion.
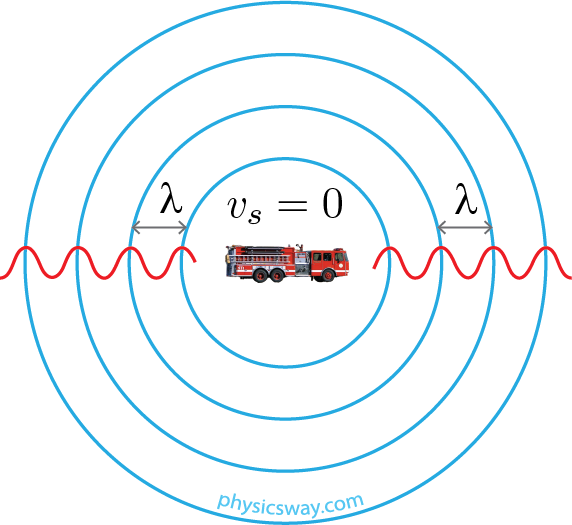
Consider a fire truck that is in rest blasts its siren. It sends out sound waves every $T$ seconds in all directions, where $T$ is the period of the sound wave. The crest of the sound waves are shown as green circles around the source in the figure. Since the truck is in rest, a new wave crest arrives in every $T$ seconds at any point in space around the truck. And, the successive crests are separated by a distance equal to the wavelength $\lambda$ of the sound. Let $v$ is the speed of the sound, which is the speed of sound in air.
Source is moving toward a stationary observer
Now, assume that the source, which is the truck is moving to the right towards a stationary observer. Let us focus our attention in front of the truck.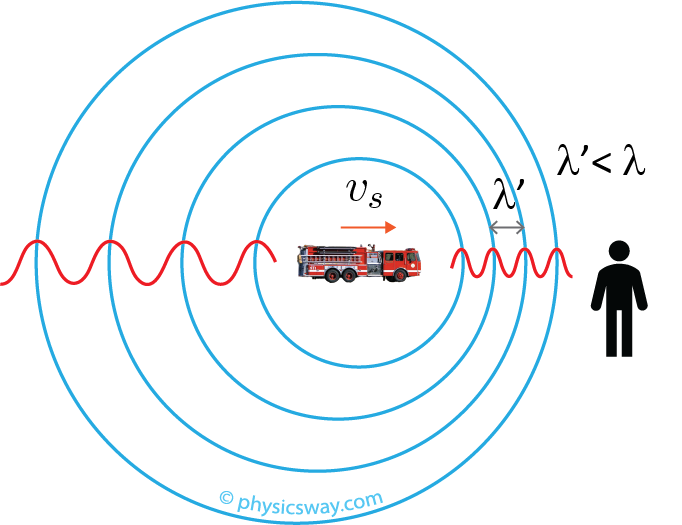
Considering one of the crest, the next crest will arrive after $T$ seconds if the truck is in rest. Since the truck is moving now, the next crest will arrive earlier than $T$. Because, before the next crest leave the source (i.e., during the time $T$) the truck moves closer to the observer by a distance, $d = v_s T$, where $v_s$ is the velocity of the source (the truck). So the crests are now closer to each other than when the source is in rest, and thus the wavelength is shorten by $d$. Smaller wavelength means, higher frequency and so the person hear a high frequency sound.
Now, let us find the frequency of the sound heard by the stationary observer.
Since the wavelength shortens by $d$, the wavelength as heard by the observer is
$\lambda'=\lambda-d$
$\:\:\:\:=\lambda-v_sT$
From $v=f\lambda$, we have
$\lambda = v/f$ and $\lambda' = v/f'$.
where $f$ is the frequency of the sound when the source is in rest and $f'$ is the perceived frequency when the source is moving.Substituting these in the previous equation,
$\dfrac{v}{f'} =\dfrac{v}{f}-\dfrac{v_s}{T}$
Since $T$ is the period of the sound wave when the source is in rest, $T=1/f$. Substituting this in the equation,
$\dfrac{v}{f'} =\dfrac{v}{f}-\dfrac{v_s}{f}$
Solving for $f'$,
$\boxed{f'=\dfrac{f}{1-\dfrac{v_s}{v}}}$
This is the frequency of sound observed by a stationary observer when the source of sound moves toward the observer. You get, $f'\gt f$, so the pitch (frequency) of the sound received by the observer is higher than the actual frequency of the sound.
Source is moving away from a stationary observer
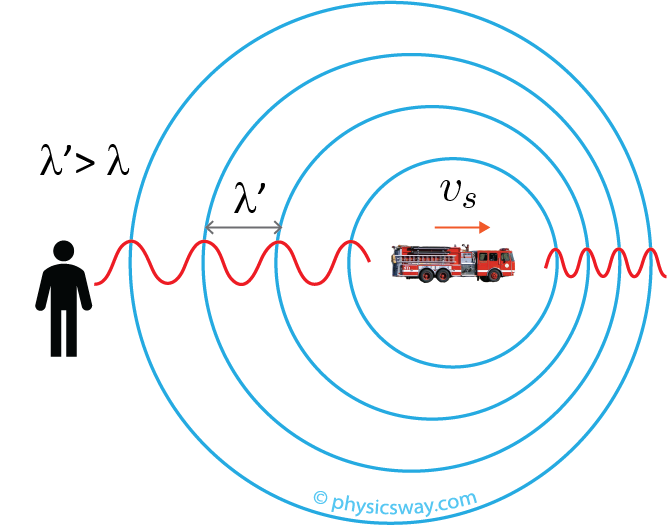
$\boxed{f'=\dfrac{f}{1+\dfrac{v_s}{v}}}$
The frequency, $f'\lt f$, so the perceived sound frequency by the observer is lower than the actual frequency of the sound.
Stationary source and the observer is moving towards the source
When the source is stationary, the wavelength of the sound from the source does not change. If the observer is moving towards the source, he/she is moving towards the waves. So, the speed of the wave relative to the observer is now, $v'=v+v_{obs}$, where $v_{obs}$ is the velocity of the observer. Therefore, the frequency of the sound as perceived by the observer is$f'=v'/\lambda$
$f'=(v+v_{obs})/\lambda$
From $v=f\lambda$, $1/\lambda=f/v$. Substituting this,
$f'=f(v+v_{obs})/v$
or$\boxed{f'=f\left(1+\dfrac{v_{obs}}{v}\right)}$
Stationary source and the observer is moving away from the source
When the observer is moving away from the stationary source, the velocity direction changes. Therefore, we need to add a minus sign to the observer velocity in the above equation to find the perceived frequency:$\boxed{f'=f\left(1-\dfrac{v_{obs}}{v}\right)}$
We can combine all the four equations that we derived in Doppler effect into one equation as follows
$f'=f\left(\dfrac{v\pm v_{obs}}{v\mp v_s}\right)$
This equation is valid, whether the source is moving, or the observer is moving or both of them are moving.
In the above equation, when source (and/or) observer move toward each other, you should have a $+$ sign in the numerator and a $−$ sign in the denominator. But when source (and/or) observer move away from each other, switch the sign, i.e., $-$ in the numerator and a $+$ sign in the denominator.
