Dynamics: Forces and Newton's laws
Dynamics is a part of mechanics. It is about studying the forces and their effects on motion. In this page you will learn about different types of forces, Newton's three laws, and applying Newton's laws to solve problems.What is a force ?
A force is a push or pull on an object. If you push an object, you are applying a force on the object. An object can exert a force on another object with a direct contact or without. A dropped object falls toward the Earth due to gravity, which is a force. Here, the Earth exerts the force of gravity on the object without any direct contact.When a force is exerted on an object, the effect of the force on the object depends on both the size (magnitude) and the direction of the force. So, force is a vector.
Newton's Laws of Motion
There are three fundamental laws of motion formulated by Isaac Newton and were published in 1687. They are called, Newton's first law, Newton's second law and Newton's third law.Newton's first law
It states that "when there is no net force acting on an object, an object in rest continues to stay in rest or an object in motion will continue its motion on a straight line".An object can be in rest or in motion, which is its state. So, changing the state of an object means, (i) if the object is in rest, we are making it to move; and (ii) if the object is in motion, we are changing its velocity. A velocity change can either be in magnitude (change in speed) or in direction. What Newton's first law says is, to change the state of an object, we must apply a net force on the object. Net force on an object is the sum of all the forces acting on the object. So, to change the speed of an object or to change the path of an object, a net force must be applied on the object. Therefore, without a net force on an object, the object will move with a constant speed on a straight line.
Any object has a resistance to change its state. That resistance is called inertia of the object. Mass is a measure of inertia of an object, because heavier the object (more mass), more force is required to change its state. Since Newton's first law is about overcoming the inertia of an object, it is also called the law of inertia.
Newton's second law
This law relates force and acceleration. Newton's second law states that "acceleration of an object is directly proportional to the net force acting on it, and inversely proportional to the object's mass."i.e., acceleration, $\vec{a}=\dfrac{\vec{F}}{m}$
where $\vec{F}$ is the net force on the object, and $m$ is the mass of the object.The first law says that to accelerate, that is to change the velocity of an object, you must apply a force (a net force) on the object. With the second law, you can calculate that acceleration.
If an object is moving with a constant velocity, then the acceleration of the object is zero. When no acceleration, the net force on the object is zero. So, a force is not required to keep an object in motion. Force is only required to accelerate an object.
Newton's second law is generally written in the following form:
$\vec{F}={m}\vec{a}$
Unit of force: The SI unit of mass is $kg$ and that of acceleration is $m/s^2$. If you multiply these two units, you will get the unit of force. So, the unit of force is $kg\cdot m/s^2$. We call this unit, newton, or $N$. So, we use newton ($N$) as the SI unit of force.
How much is $1N$ of force ? It is the force required to accelerate a $1kg$ object by $1m/s^2$. For example, if there is a $1 kg$ ball at rest on the ground and you give a kick to the ball so that in $1s$ the ball attains a speed of $1 m/s$, then you have applied a force of $1 N$ on the ball.
Newton's second law in components form
Since force is a vector, the $x$ and $y$ components of a force are independent. So, if an object is moving on the $x$ axis, only the $x$ component of the net force affects the motion. Likewise, the motion on the $y$ axis. So, we can write the Newton's second law in components form as$F_x={m} a_x$ and $F_y={m} a_y$
where $F_x$ and $F_y$ are the $x$ and the $y$ components of the net force on the object, and $a_x$ and $a_y$ are the $x$ and the $y$ components of the object's acceleration.Newton's third law
It states that "whenever an object exerts a force on a second object, the second object exerts an equal amount of force on the first in the opposite direction."Newton's third law can also be stated as, "for every action there is an equal and opposite reaction."
According to Newton's third law, force always acts in pair: force and its reaction force. The magnitudes of the force and the reaction force are the same regardless of the size (mass) of the objects involved. For example, if a small car and a big truck involve in a collision, whatever the force the truck exerts on the car during the collision is same as the force the car exerts on the truck, but the direction of the forces are opposite. Although the forces are the same, the smaller object is accelerated at a higher rate due to its smaller mass according to Newton's second law.
Force of gravity (weight)

$\vec {F}=\vec{F_g}$
Applying Newton's second law, $\vec F = m\vec a$, we get
$\vec {F_g}=m\vec{a}$
where $m$ is the mass of the object and $\vec a$ is its acceleration.
You learned in kinematics that any falling object near the surface of the earth has an acceleration of magnitude, $g$. Since the acceleration is downward, it is negative taking the positive upward:
$\vec a= -g$
Substituting this in the above equation, we get,
$\vec {F_g}=-m g$
The sign of the force of gravity depends on how you choose the direction. It is negative as I take the positive upward. But the magnitude of the force of gravity is a positive number that is
$\boxed{F_g=m g}$
When a falling object hits the ground, the earth doesn't stop puling the object. Earth still pulls the object with the same force but the earth's surface keep it from moving further. So, the force of gravity is always acting on an object, whether the object is in motion or in rest. Force of gravity is also called, weight. So, weight and mass are not the same as weight is a force, mass is not.
Normal force
If you have an object on a horizontal surface in rest, then the net force acting on the object is zero. But, you know that there is a force of gravity acting on the object in the downward direction. Since the net force on the object is zero, there must be a vertical force acting on the object to cancel the downward gravitational force. That upward force is called normal force, $\vec F_n$.Normal force acts perpendicular to the surface. On a horizontal surface, the normal force balances the force of gravity and keeps the object from falling down further.
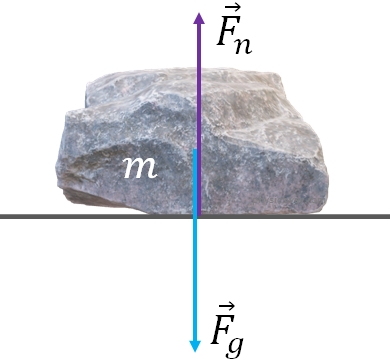
So, on a horizontal surface, with no other forces except the force of gravity acting on the object, the magnitude of the normal force is equal to the weight of the object:
$F_n=mg$
Scale reading and normal force
Assume you have placed an object on a scale. The scale shows some reading. Now, slightly push the object downwards with your finger(s), you will see the scale read more than that was before. And, if you grab the object with your hand, and slowly pull it upward, you will see the scale reading gets smaller than before. These show us that what the scale reads is not always the actual mass of the object. So, what the scale reads then?.
What a scale reads is the normal force. That is the normal force exerted on the object by the surface of the scale. When you are pushing or pulling the object, you are applying a force on the object that changes the normal force, so you see different scale readings. Normal force is called the apparent weight of the object. Scales (such as a bathroom scale) are calibrated to show the mass in $kg$ or $lb$ that is nothing but the normal force divided by $g$. Note that the mass,$m$ of an object does not change, but the reading of mass on the scale changes. So, we call the mass as read by a scale, the apparent mass, $m'$. The apparent mass is
$m'=\dfrac{F_n}{g}$.
If the scale plus the object are in rest or they are moving at a constant speed (read below for more understanding), and no other forces acting on the object, then the scale reads the actual mass of the object, $m'=m$.
Apparent weight in an elevator
If you were ever in an elevator, you might have noticed that when the elevator starts moving upward from rest, you feel more weight than you normally does. Further, when the elevator is moving downward from rest, you feel less weight than normal. And, when the elevator is settled and moving with a constant speed, you don't feel any difference in weight. The reason is the weight you feel is the normal force exerted on you by the surface of the elevator. When the elevator is at rest or moving at a constant speed, the normal force by the elevator surface is your actual weight. When the elevator is accelerating upward, the normal force is greater than the actual weight, and it is smaller when the elevator is accelerating downwards. The following problem proves these.
Problem: A scale is in an elevator and a $55kg$ woman is standing on the scale. Determine what the scale will read
(A) if the elevator ascends with an increasing speed at a rate of $2.1m/s^2$,
(B) if the elevator descends with an increasing speed at a rate of $2.1 m/s^2$ and
(C) if the elevator is moving at a constant speed (upward or downward).
Solution: To solve this problem, first step is drawing a free body diagram. The object in this problem is the woman, so we need to consider all the forces acting on her.
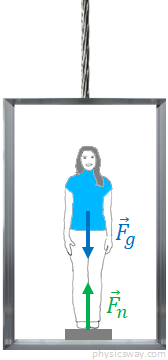
There are two forces acting on the woman, the force of gravity (the weight) and the normal force by the surface of the scale. Both the forces are in the vertical direction: the normal force, vertically upward and the gravity in the vertically downward direction. Taking the positive upward, the net force on the woman is
$F=F_n-mg$
Applying the Newton's second law, $F=ma$, we get
$F_n-mg=ma$
where $a$ is acceleration of the woman that is the acceleration of the elevator as both the woman and the elevator are moving together as one unit.
This is the main equation for an elevator problem.To find the scale reading, we need the normal force. From the equation,
$F_n=mg+ma$
Now let us consider the cases.
(A) The elevator ascends with an increasing speed at a rate of $2.1m/s^2$.
Here the elevator is moving upward. Since we take positive upward, the elevator is moving in the positive direction. The elevator is speeding up, therefore the direction of acceleration is same as the direction of motion of the object (the elevator), which is the positive direction. So, the acceleration is positive:
$a=+2.1 m/s^2$
$m=55kg$, the mass of the woman.
All the quantities are in SI units. By substituting the known values, we can find the normal force:
$F_n=55 \cdot 9.80 +55\cdot 2.1$
$=654.5 N$
Since the scale reads in $kg$, divide the normal force by $g$ to get the scale reading in $kg$.
$m'=\dfrac{F_n}{g}$
$=\dfrac{654.5}{9.80}$
$=67\, kg$
You see that the scale reading is more than the mass of the woman. That is why you feel heavier when the elevator starts moving upward, i.e., the elevator is accelerating upward.
(B) The elevator descends with an increasing speed at a rate of $2.1 m/s^2$.
In this case, the elevator is moving downward and is speeding up, so the acceleration direction is downward in the negative direction:
$a=-2.1 m/s^2$
Substituting the values in the $F_n$ equation, you will get,
$F_n=55 \cdot 9.80 +55\cdot (-2.1)$
$=423.5 N$
And the scale reading is
$m'=\dfrac{423.5}{9.80}$
$=43\, kg$
(C) the elevator is moving at a constant speed (upward or downward).
When the elevator is moving upward (or downward) with a constant speed, its velocity is constant as the direction is constant. So, the acceleration of the elevator (and the woman) is zero:
$a=0$.
Substituting this in the normal force equation:
$F_n=mg+m\cdot 0$
$=mg$
Therefore, $m'=\dfrac{F_n}{g}=m= 55\, kg$
That is the scale reading is the actual mass. So, when the elevator is moving at a constant speed, you do not feel any difference in your weight.
Tension or force of tension
If you use a flexible cord to pull an object, then you are applying a force to the object via the cord. Such a force is called force of tension or just tension, $\vec F_t$. Tension is a pulling force transmitted through a flexible chord such as a cable, rope or a chain.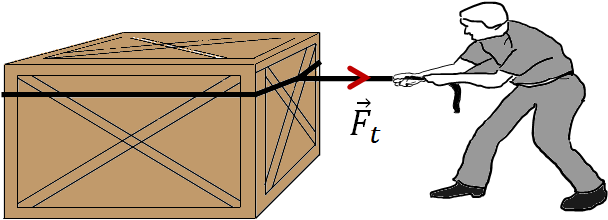
Free body diagram
When you are dealing with problems in dynamics, the first step is to draw a diagram that shows all the forces acting on the object. Such a diagram is called a free body diagram or a force diagram. The diagram should show the directions of the forces with arrows and their approximate magnitudes (by the length of the force lines).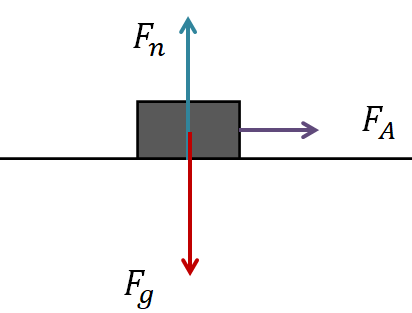
In the above, there is only one object. Sometimes, you may have a system that contains more than one object. If there is more than one object, then draw the force diagram for each object separately, and apply Newton's second law for each.
Solving problems with Newton's second law
To apply the Newton's second law, you need to add all the forces acting on the object to get the net force. Remember that force is a vector, so you need to do vector addition when adding forces. If there is more than one force acting on the object, you need to work with the forces on each axis separately. Since, the $x$ and the $y$ components of a force is independent, the net force on the object along the $x$ direction affects only the motion in that direction, and so the $y$ direction. So, you need to apply the Newton's second law on each axis separately:$F_x=ma_x$ and
$F_y=ma_y$
where $F_x$ and $F_y$ are the net forces along the $x$ and the $y$ direction; $a_x$ and $a_y$ are the acceleration of the object in the $x$ and the $y$ direction.
If an object is moving on the $x$ axis, then there will be no motion on the $y$ axis, therefore, $a_y=0$. And if the object is moving on the $y$ axis, then $a_x$=0. Further, you are free to ignore the subscript in the acceleration, if the object is moving on one of the axes.
If a force is neither along the $x$ axis nor along the $y$ axis, then find the $x$ and the $y$ components of that force, and work with those components.
Example:You have a box of mass 11 kg and is pulled by a force, $\vec F_p = 32 N$ at an angle of 25 degrees above the horizontal. The box is moving on the floor.(a) find the normal force on the box, and
(b) find the acceleration of the box.
Solution:
First, draw the $x$ and the $y$ axes. Then draw all the forces acting on the object, which is the free body diagram.
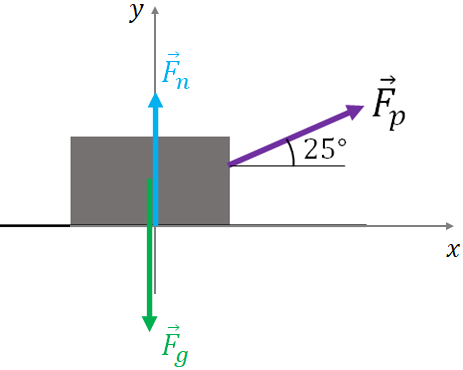
There are three forces acting on the object. The force of gravity, the normal force by the surface and the applied (pulling) force.
Second, check if all the forces are in the $x$ or $y$ direction. If a force is not along one of the direction, then you need to find its $x$ and $y$ components as those components will be in the $x$ and the $y$ direction respectively.
$F_n$ and $F_g$ are along the $y$ axis. Since, the pulling force, $\vec F_p$ is neither along the $x$ axis nor along the $y$ axis, you need to find its $x$ and $y$ components. Drawing the components of $\vec F_p$, we get,
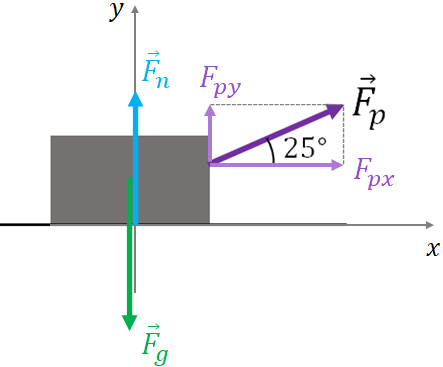
From the figure, we can write,
$F_{px}=F_p \cos (25)= 32 \cos(25)=29N $
and$F_{py}=F_p \sin (25)= 32 \sin(25)=13.52N $
(a) Finding the normal force:
Since the normal force is along the $y$ axis, you need to add all the forces (or components) in the $y$ direction and apply the Newton's second law. Note that $y$ direction means both the positive and the negative directions of $y$.
Net force in the $y$ direction is
$F_y=F_n-mg+F_{py}$
I put a $-$ sign for the force of gravity as it is downward and $+$ sign for $F_{py}$ as it is upward.Now, applying Newton's second law:
$F_y=ma_y$
Since there is no motion of the box along $y$ direction as it is moving in the $x$ direction , $a_y=0$. Putting this in the equation, we get,
$F_y=0$
Substituting $F_y$ from the previous equation,
$F_n-mg+F_{py}=0$
Solving for $F_n$
$F_n= mg-F_{py}$
Substituting the values of $m$, $g$ and $F_{py}$,
$\boxed{F_n=94N}$
Note that the pulling force changes the normal force on the box as if there is no pulling force, then
$F_n=mg=110 N$ after rounding to correct significant figures.
So, here, the pulling force reduces the normal force.(b) Finding the acceleration:
Since the motion of the box is in the $x$ direction, you need to add all the forces in the $x$ direction (positive or negative $x$ direction) and apply the Newton's second law in that direction. There is only one force in the $x$ direction, which is $F_{px}$. So, the net force in the $x$ direction is $F_{Px}$:
$F_x=F_{px}=29N$
Applying Newton's second law:
$F_x=ma_x$
Substituting the values and solving for $a_x$,
$\boxed{a_x= 2.6 m/s^2}$.
Two hanging masses over a pulley
Here, there are two masses, $m_1$ and $m_2$ hanging from a rope and the rope runs over a pulley. Assume, $m_2 > m_1$.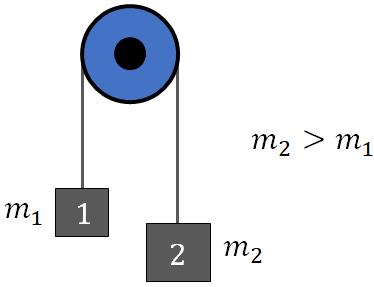
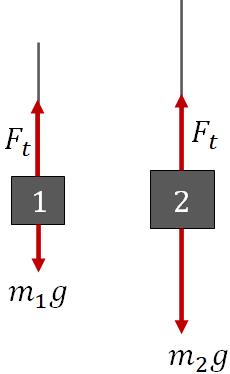
We are going to find the acceleration of the masses and the tension on the rope. Since the two masses are connected together with a rope, both have the same magnitude of acceleration, $a$. But the directions of the acceleration are different. If we take positive upward, then the acceleration of mass 1 is positive and that of mass 2 is negative:
$a_1=a$ and $a_2=-a$
All the forces are in the vertical direction: upward or downward. That is the forces are only along the $y$ axis. So we just need to consider the net force on each object along the $y$ axis.
For object 1, the net force on it is
$F_t-m_1g=m_1a_1$
Substituting $a_1=a$,
$F_t-m_1g=m_1a$ (1)
For object 2, net force is
$F_t-m_2g=m_2a_2$
Substituting $a_2=-a$,
$F_t-m_2g=-m_2a$ (2)
Solving equations (1) and (2) for $a$ and $F_t$ we get,
$a=g\, \dfrac{m_2-m_1}{m_1+m_2}$
and$F_t=\dfrac{2g\, m_1 m_2}{m_1+m_2}$
Note that when $m_1=m_2$, $a=0$ and there is no motion of the masses.
Friction
When you try to slide an object on a surface, the microscopic bumps on the surface impede the motion. If the surface is smooth, you need less force to move the object, but a rough surface requires more force. Friction is a resistance that results from the microscopic bumps on a surface. It prevents an object in rest from moving when applying a force. If the object is in motion, then friction acts in the direction opposite to the direction of motion and try to stop the motion. Friction is a force that acts parallel to the surface.Static friction
Assume, you have an object on a horizontal surface in rest. You are trying to move the object by applying a horizontal force,$\vec F_A$ . Your force is not strong enough that the object is not moving. Since the object is in rest, the net force on the object must be zero. Now you can realize that there must be another horizontal force of same magnitude as the applied force acting on the object in the opposite direction so that the net force is zero. This opposing force is the force of friction. Since the object is not moving, we call this friction static friction. Static friction prevents an object from moving when applying a force.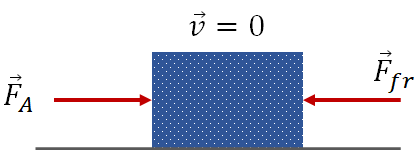
If you increase the applied force, friction also increases and balances the applied force, until the object starts moving. So, when the object is not moving, the magnitudes of the applied force and the friction force are equal:
$F_{fr}=F_A$, if the object is not moving.
If you keep on increasing the force, and at one point, the object starts moving. The force you apply when the object just starts moving is the maximum friction.
Experimentally it has been found that the magnitude of the maximum friction is proportional to the normal force on the object by the surface:
i.e., $(F_{fr})_{max}=\mu_sF_n$
where $\mu_s$ is called the coefficient of static friction between the object and the surface. $\mu_s$ depends on the surface and the object.
Kinetic friction
If the applied force on an object exceeds the maximum friction, then the object starts moving. Once the object start moving, friction reduces by some amount. Force of friction acting on an object in motion is called kinetic friction. Kinetic friction acts in the direction opposite to the direction of motion.
Kinetic friction is proportional to the normal force exerted on the object by the surface:
$F_{fr}=\mu_kF_n$
where $\mu_k$ is the coefficient of kinetic friction between the object and the surface.
$\mu_s$ is always greater than $\mu_k$.
Smooth surfaces:
We will use the term "smooth surface" to refer to a surface that has no friction. So, on a smooth surface, $\mu_s=0$ and $\mu_k=0$. We ignore the friction force on an object on a smooth surface. Note that in reality, there is no perfectly smooth surface.
Inclines
An incline is a flat surface tilted relative to the horizontal. One end of the incline is higher than the other. In the figure below, an object is on an incline. The angle of the incline is $\theta$, which is the angle of the surface from the horizontal.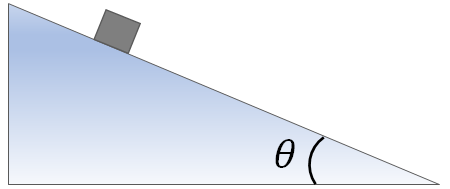
You learned that the normal force of an object on a surface is perpendicular to the surface. If the surface is horizontal, then the normal force is in the vertically upward direction. Since an incline surface is not horizontal, the normal force is not vertical.
Force diagram for an object on a smooth (no friction) inclined surface is given the following figure. The normal force and the force of gravity on the object is shown in the picture below. Remember that the force of gravity always acts vertically downward no matter where the object is. As usual, we still take the normal force is along the $y$ axis, and the $x$ axis is along the inclined surface.
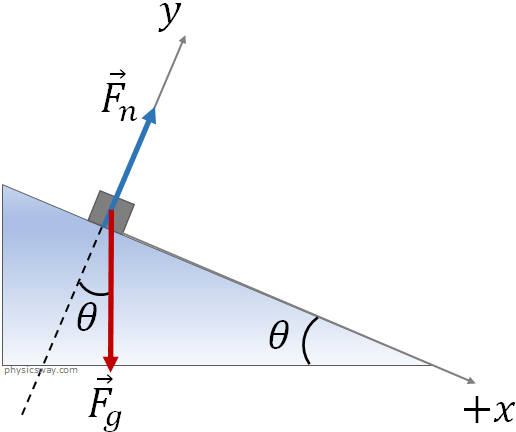
We always work with forces that are on the $x$ and the $y$ axes. Here, the normal force is on the $y$ axis, but the force of gravity is neither along the $y$ axis nor along the $x$ axis. So, we will find its $x$ and $y$ components.
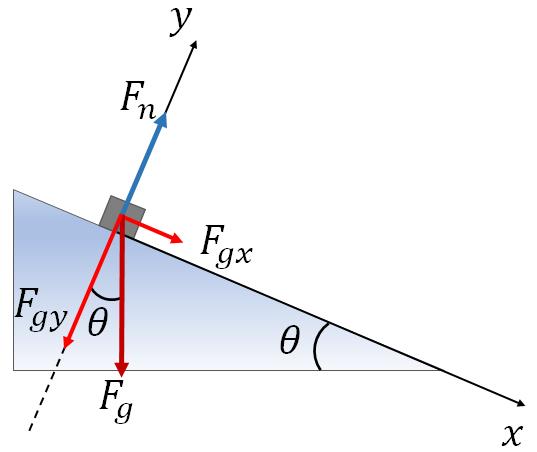
From the geometry of the figure, the $x$ and the $y$ components of the force of gravity are,
$F_{gx}=mg\sin\theta$
$F_{gy}=-mg\cos\theta$
On an incline, motion of the object if any takes place only along the $x$ axis, and no motion along the $y$ axis. Therefore, the net force along the $y$ axis is zero.
So, adding all the forces along the $y$ axis, we get,
$F_n-mg\, \cos\theta=0$
or$F_n=mg\cos\theta$.
Objects in rest on an incline:
An incline may be a frictionless (smooth) surface or may have friction. If there is no friction, then an object cannot be in rest on an incline as the force of gravity on the object will bring it down. So, there must be a friction force between the object and the surface for the object to sit. On the $x$ axis, there are two forces acting on the object, the $x$ component of the force of gravity, $F_{gx}$ that acts in the downhill and the friction, which acts opposite to the $F_{gx}$. The $F_{gx}$ should be smaller than the maximum static friction, otherwise the object will slide down. When the object is in rest, the friction force balances $F_{gx}$. So the magnitude of the friction force on the object is$F_{fr}=mg\sin\theta$.
This is the friction force on an object in rest on an incline.
Object's motion on an incline:
On an incline, an object can be either sliding down from the top by releasing it or going up from the bottom by giving some initial velocity to the object (i.e., the initial push).Object is sliding down: The free body diagram of the object that is sliding down is given below. When the object is sliding down, the force of friction acts toward the uphill to impede the motion.
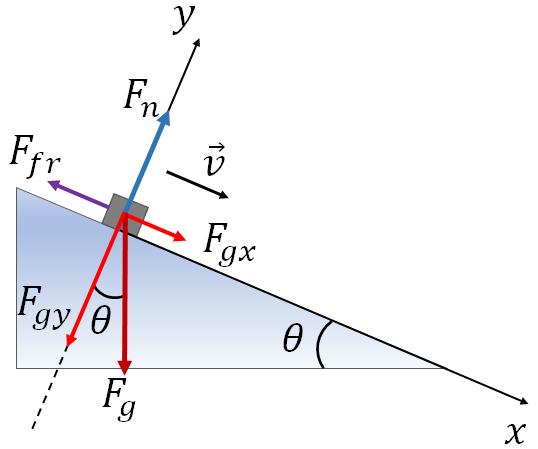
Applying Newton's second law along the $x$ axis, we have
$-F_{fr}+mg\sin\theta=ma$
Note that I have taken the downhill as the positive $x$ direction.You can find the magnitude of the friction force by using the equation:
$F_{fr}=\mu_k\:F_n$.
Substituting $F_n$ for an incline:
$F_{fr}=\mu_k\:F_n=\mu_k\:mg\cos\theta$.
Substituting this in the above equation and dividing out the mass, $m$, you will get,
$a=-\mu_k\:g\cos\theta+g\sin\theta$
This is the acceleration of the object that is sliding down.
Object is sliding up:
If you give an initial push to an object that is at the bottom of an incline, then it can move uphill on the incline. Since the friction always acts in the direction opposite to the direction of motion, the friction acts in the direction toward the downhill. So, the friction force is now positive. As a result, the first term in the acceleration is positive now:$a=\mu_k\:g\cos\theta+g\sin\theta$
This is the acceleration of the object that is sliding up.
