Fluids

There are four phases of matter: solid, liquid, gas and plasma. Liquids, gases and plasmas are called fluids. A fluid can be compressible or incompressible. Fluids whose volume cannot be reduced by applying pressure are called incompressible fluids. Liquids are incompressible fluids, but gases are not.

Density

Density $\rho$ of a substance is defined as mass per unit volume.

$\rho=\dfrac{m}{V}$

where $m$ is the mass of the substance and $V$ is its volume. SI unit of density is $kg/m^3$.

Density of water is $1000 \,kg/m^3$.

Pressure

Force exerts pressure on the surface of an object. Pressure is defined as force per unit area. If a force of magnitude, $F$ is applied on a surface of area $A$, then the pressure $P$ exerted on the surface by the force is:

$P=\dfrac{F}{A}$

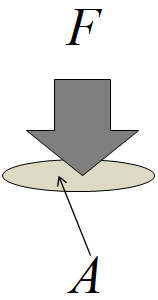
SI unit of pressure is $N/m^2$ or pascal (Pa).

Pressure in fluids

In fluids, pressure increases with depth. When you go from the surface to a depth $h$, the pressure of the fluid increases by an amount:

$\Delta P=\rho g h$

where $\rho$ is the density of the fluid.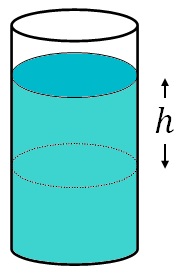

The proof of the above equation is as follows.

Consider a cylindrical container containing some liquid of density, $\rho$. Let $A$ is the area of cross section of the container (cylinder). To find the pressure at depth $h$, assume an imaginary surface at that depth. On this imaginary surface, the force acting on is the weight of the column of the fluid above it. So, the pressure on the imaginary surface is due to the force that is the weight of the column of the fluid of height, $h$.

$F=W=mg$

where $m$ is the mass of the fluid of column of height $h$.

Mass can be written as, $m=\rho V$, where $V$ is the volume of the fluid column of height $h$.

So, $F=\rho V\,g$

The volume, $V$ is the volume of a cylinder of height, $h$:

$V=Ah$

Substituting this,

$F=\rho Ah\,g$

Now, the pressure on the imaginary surface at a depth $h$ is

$\Delta P=\dfrac{F}{A}$

$=\dfrac{\rho Ah\:g}{A}$

$\boxed{ \Delta P=\rho g h}$

This equation shows that the pressure in a fluid depends on the depth and is independent of the shape of the container. If you take any container of any shape you will get the same result. So, pressure increases as depth increases in fluids. At a given depth, pressure is same at all points. Further, an object in a fluid experiences pressure from all directions, not only from the top.

Atmospheric pressure

Earth has an atmosphere. On the surface of the earth, there is a pressure due to the weight of the atmospheric gases above the surface. This pressure is called atmospheric pressure. At the sea level, atmospheric pressure, $P_{atm}$ is,

$P_{atm}=1.013\times 10^5 N/m^2$

We call this pressure, $1\:atm$

i.e., $1\:atm=1.013\times 10^5 N/m^2$

Absolute and gauge pressure

If you measure the tire pressure of a flat tire with a gauge, it will show you a reading of zero. It doesn't mean that there is no air pressure inside. There is still pressure inside the tire that is same as the atmospheric pressure. But the tire gauges measure only the pressure difference between the tire and the atmosphere. The pressure measures by a gauge such as a tire pressure gauge, is called the gauge pressure. To find the absolute pressure of a system, you need to add the atmospheric pressure to the gauge pressure of the system. Therefore,

Absolute pressure = atmospheric pressure + gauge pressure

Note that all the pressure differences are gauge pressure as they do not include the atmospheric pressure. For example, the pressure difference in a fluid at a given depth and the surface is a gauge pressure as it does not include atmospheric pressure.

Pascal's principle

If an external pressure is applied to a confined fluid, then the pressure at every point within the fluid increases by that amount. This is called Pascal's principle.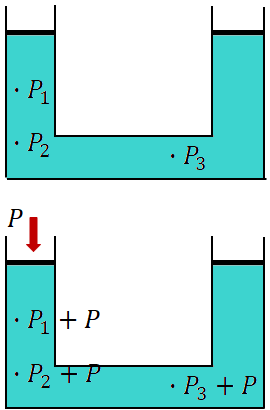

Here, I have a confined fluid. The pressure at different points are shown. Now, if I apply an external pressure, $P$ to one part of the fluid by a piston, then the pressure at each point increases by $P$.

Pascal principle is applied in hydraulic brakes and in hydraulic lifts. Hydraulic lifts are used to lift heavy objects with little force. With those machines, you can amplify the forces.

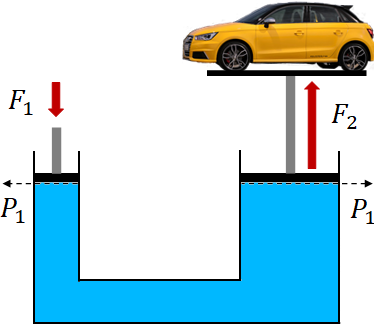
In a hydraulic lift, there is a confined fluid with two pistons, a smaller and a larger one on either side.

Now, when you apply a force on the smaller piston, you are applying a pressure on the fluid that is

$P_1=\dfrac{F_1}{A_1}$

where $A_1$ is the area of cross section of the smaller piston.

According to Pascal's principle, the pressure at all points in the fluid increase by $P_1$. So, the pressure by the fluid on the larger piston also increases by $P_1$.

This pressure exerts a force, $F_2$ on the larger piston,

$F_2 = P_1 A_2$

where $A_2$ is the area of cross section of the larger piston.

Substituting $P_1$, we get

$F_2 = \dfrac{A_2}{A_1} F_1$

The force at the larger piston depends on the areas of cross section of the two pistons. By increasing the ratio, $A_2/A_1$, we can increase the force at the larger piston, so that heavier object can be lifted. For example, if the cross sectional area of the larger piston is 4 times that of the smaller piston, then the force at the larger piston will be 4 times that of the force applied to the smaller piston: $F_2=4F_1$.

Pressure measurement

There are several instruments to measure pressure, such as manometer, aneroid gauge and barometer. Barometers are used to measure the atmospheric pressure.

Open tube manometer

It is a U-shaped tube with one end (on the left side) open to the atmosphere and the other end (on the right side) is connected to the system that you want to measure its pressure. The tube is filled with some fluid of density $\rho$. Depends on the pressure, $P$ of the system, there is a height difference between the fluid level in the left and the right side of the tube.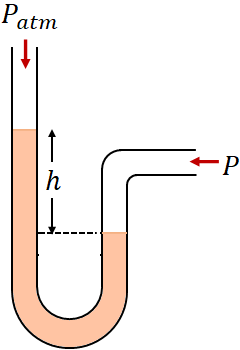

The left top surface of the fluid is at the atmospheric pressure as it is open. And the right top surface of the fluid is at the unknown system's pressure. Since pressure in a fluid is same for the same height (or depth), the pressure within the fluid at a depth $h$ on the left side of the tube is same as that of the pressure at the top of the fluid in the right side. So, the pressure difference between the top of the fluid and at depth $h$ on the left side of the tube is

$\Delta P=P-P_{atm}=\rho gh$

(or)

$P=P_{atm}+\rho g h$

This is the absolute pressure of the system.

Mercury barometer

Mercury barometer is used to measure the atmospheric pressure. It consists of a long tube filled with mercury and is inverted in a beaker containing mercury. Once the tube is inverted, mercury level drops until the weight of the mercury column above the surface of the beaker is balanced by the upward force by the atmospheric pressure. There is a vacuum created at the top of the inverted tube. So, the top of the column is at zero pressure.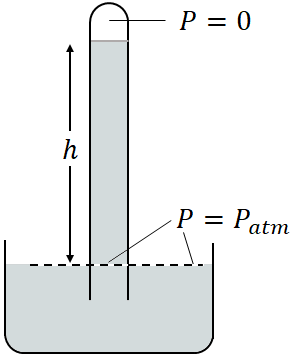

Inside the column, the pressure at the level of the dotted line is same as the pressure of the mercury surface in the beaker that is at the atmospheric pressure. Therefore the pressure difference between the bottom and the top of the column is

$\Delta P =P_{atm}-0=\rho gh$

$P_{atm}=\rho gh$

where $\rho$ is the density of mercury.

The height of the mercury changes with the atmospheric pressure. At a pressure of $1\, atm$ the height of the mercury column will be $76\:cm$.

If water is used instead of mercury, the height of the water column will be $10.3m$ and you will need a very long tube. But with mercury we can have a compact barometer due to its high density. That is why mercury is preferred over other liquids in barometers.

Buoyancy

Objects such as wood float in water and objects weigh less in water and can be easily lifted. Why?. It is due to a phenomenon called buoyancy.

You learned that pressure in a fluid changes with depth. So, an object immersed in a fluid, experiences higher pressure at its bottom than that at its top. Due to the fluid pressure, there are forces exerted on the surface of the object. On the top surface, fluid exerts a downward force, $\vec F_1$ and the bottom surface an upward force, $\vec F_2$. Since the pressure is higher at the bottom than at the top, $F_2>F_1$. As a result, there is a net upward force acting on the object. This net upward force is called the buoyant force, $F_B$.

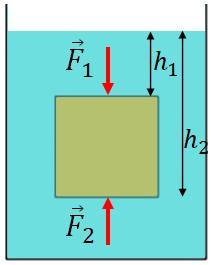
The buoyant force is

$F_B=F_2-F_1$

Archimedes principle

Archimedes in 250 B.C suggested that the buoyant force on an object in a fluid is equal to the weight of the fluid displaced by the object:

$F_B=m_f \,g$

where $m_f$ is the mass of the fluid displaced by the object and $g$ is the acceleration due to gravity.

If $V_{disp}$ is the volume of the fluid displaced by the object, then

$m_f=\rho_fV_{disp}$

where $\rho_f$ is the density of the fluid.

Archimedes principle is valid whether the object is submerged or floating in the fluid.

If the object is submerged in the fluid, then $V_{disp}$ is the volume of the object. And, if the object floats, then $V_{disp}$ is the volume of the object within the fluid.

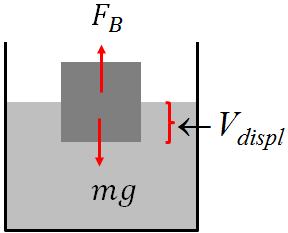
If an object has less density than a fluid, then the object floats in that fluid. When an object floats, the buoyant force on the object balances the weight of the object. So, for a floating object,

$F_B=mg$

where $m$ is the mass of the object.

If the weight exceeds the buoyant force, then the object sinks.

Apparent weight of an object

In fluids, an object weighs less than its actual weight due to the buoyant force. The weight of an object in a fluid is called its apparent weight.

Apparent weight of an object in a fluid is

$w'=mg-F_B$

Fluid dynamics or hydrodynamics

When fluid flows, the flow can be smooth, called streamline or laminar flow or erratic (not smooth), called turbulent flow. In a laminar flow, each path of the particle (streamline) does not cross each other and the neighboring layers of the fluid slide by each other smoothly. In a turbulent flow, whirlpool-like circles forms in the fluid at higher speeds. Laminar flow is easy to study, and here we will focus on the fluid flow that is laminar.

Flow rate

The amount of fluid flows per unit time across a cross sectional area is called the flow rate of the fluid. There are two types of flow rates: volume flow rate and mass flow rate.

Volume flow rate

Volume flow rate is the volume of the fluid that passes through a given cross sectional area per unit time,

Volume flow rate $= \dfrac{\Delta V} {\Delta t}$

where $\Delta V$ is the volume of the fluid passing through a cross section of the tube in a time $\Delta t$.

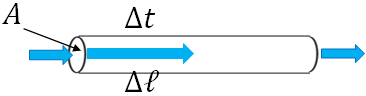
If a fluid flows with velocity $v$ through a tube of area of cross section $A$ , then the volume flow rate of the fluid is

Volume flow rate$=Av$

You can prove this as follows. Consider a uniform diameter tube of area of cross section $A$. Choose a cross section anywhere in the tube. Now, let us consider a time $\Delta t$, and during which, the liquid travels from the chosen cross section to a distance $\Delta \ell$. So, during the time, $\Delta t$, the volume of water leaves the cross section is the volume of a cylinder of area of cross section $A$ and height, $\Delta \ell$:

$\Delta V = A\Delta \ell$

So, the volume flow rate is

Volume flow rate $=\dfrac{\Delta V}{\Delta t}=A\Delta l/\Delta t$

$\Delta l/\Delta t$ is nothing but the speed of the fluid, $v$. Therefore,

Volume flow rate, $\dfrac{\Delta V}{\Delta t}=Av$

Mass flow rate

Mass flow rate is the mass of the fluid passing through a given cross sectional area per unit time.

i.e., Mass flow rate $= \dfrac{\Delta m} {\Delta t}$

where $\Delta m$ is the mass of the fluid passing through a cross section of the tube in a time $\Delta t$.

If $\Delta V$ is the amount of the fluid passing through a cross section of the tube in a time $\Delta t$, then using the density, mass and volume relation,

$\Delta m= \rho \Delta V$

Substituting this

Mass flow rate $= \dfrac{\rho \Delta V} {\Delta t}$

Substituting, $\dfrac{\Delta V}{\Delta t}=Av$, we get

Mass flow rate, $\dfrac{\Delta m}{\Delta t} =\rho A v$

Equation of continuity

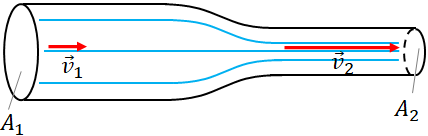
The figure above shows that a fluid flows through a pipe. There are two sections in the pipe, the section on the left has larger diameter with area of cross section, $A_1$ and the section on the right has smaller diameter with area of cross section, $A_2$. Whatever the fluid enters the larger diameter section should leave through the smaller diameter section as there is no other path. So, the mass of the fluid enters one section of the fluid in a given time should leave the other section of the tube. In other words, the mass flow rate in both the sections are the same:

$\dfrac{\Delta m_1}{\Delta t}=\dfrac{\Delta m_2}{\Delta t}$

where the left hand side is the mass flow rate in the larger diameter section and the right hand side is that in the smaller diameter section.

Substituting, $\dfrac{\Delta m}{\Delta t}=\rho Av$, we get

$\rho_1 A_1v_1=\rho_2 A_2v_2$

where $\rho_1$ is the density of the fluid in the bigger diameter section and $\rho_2$ is that of the smaller diameter section.

If the fluid is incompressible, such as liquids, then the density does not change, therefore,

$\rho_1=\rho_2$, and the above equation becomes,

$A_1v_1=A_2v_2$

This is called the equation of continuity.

i.e., When an incompressible fluid flow through a tube of varying cross section (diameter), its volume flow rate is constant.

Bernoulli's principle

Bernoulli's principle relates velocity and pressure of a fluid. It states that where the velocity of a fluid is high its pressure is low and where the velocity is low, the fluid pressure is high.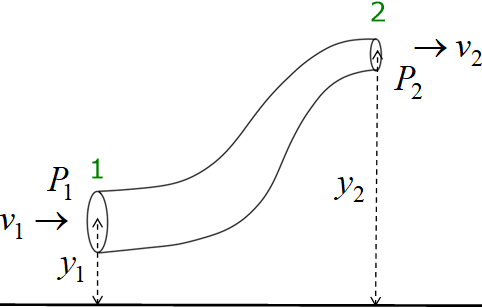

A fluid flowing through a pipe is shown in the figure. We are considering two regions of the pipe, 1 and 2. The height of the pipe at region 1 is $y_1$ and that of the region 2 is $y_2$. Let $P_1$ and $P_2$ are the pressure at the regions 1 and 2, and $v_1$ and $v_2$ are the velocities in those regions.

Bernoulli showed that at any point in the fluid,

$P+\dfrac{1}{2}\rho v^2+\rho g y\:$ is a constant.

i.e., $P_1 + \dfrac{1}{2} \rho v_1^2 + \rho\, g\, y_1$ $=P_2+\dfrac{1}{2}\rho v_2^2+\rho\, g\, y_2$.

This equation is called Bernoulli's equation.

Bernoulli's equation is a law of conservation of energy involving fluid flow.