Special theory of relativity

Special theory of relativity is a theory, which relates space and time. It was proposed by Albert Einstein in 1905.

Inertial reference frame

We do measurements such as displacement, velocity and acceleration of an object relative to a reference called reference frame or frame of reference. And, we use the x-y-z coordinate system as the reference frame. For example, to find the velocity of a car moving on a road, we choose a fixed point described by the coordinate system and find the displacement of the car from that point. Then, divide the displacement by the time the car took for that displacement to get the velocity. Since, the reference frame is fixed somewhere on the ground, we say, the ground is the reference frame. Now, assume a person is running inside a train. And, another person who is sitting in the train measures the velocity of the running person. For this velocity, train is the reference frame as he/she chooses the fixed point in the train for the measurement.

If a reference frame that is at rest or moving with a constant velocity, then it is called an inertial reference frame. So, an inertial reference frame does not accelerate.

Postulates of special theory of relativity

There are two postulates of special theory of relativity. They are called postulate 1 and postulate 2.

Postulate 1: The laws of physics have the same form in all inertial reference frames.

For example, assume a car is in motion on a straight road. Here, the reference frame is the ground that is in rest. To study the motion of the car, we use the kinematic equations. Now, consider a warfare ship that is moving with a constant velocity on a ocean, and on its landing platform a car is in motion. Here, the reference frame (the ship) is an inertial reference frame as the ship is moving with a constant velocity. So, a person in the ship can use the same kinematic equations to study the motion of the car on the ship. So, according to the first postulate, all the inertial reference frames are the same and we can use all the laws of physics in its form to study the kinematics or dynamics of objects.

You can realize the first postulate in everyday life as well. This is because, whatever you do on earth can be done without seeing any difference by sitting on an airplane or a train that is moving with a constant velocity. For example, if you stand on the ground and drop a ball, the ball will follow a straight line and will hit the ground exactly below where it was. The same thing happens if you drop the ball while standing on a train that is moving with a constant velocity. The ball will hit the floor of the train exactly below the point from it was dropped.

Postulate 2: Speed of light is a universal constant that does not change with the speed of the source or the observer.

Assume a cannon is in rest shoots balls, and each cannon ball leaves the cannon with some speed, say $v_b$. Now, the cannon starts moving with some speed, say $v_c$ in the same direction as the cannon balls leave the cannon. Since both the cannon and the balls move in the same direction, the velocities are added up. So, now the speed of the cannon balls is $v_b+v_c$. And, if the cannon moves in the opposite direction to the balls, then the speed of the cannon balls will be $v_b-v_c$. This tells you that the speed of the cannon balls depends on the speed of the source, the cannon. This is true not only for objects like cannon balls, but also true for waves such as sound waves. Further, when you are driving on a freeway, and if a car is approaching you, you observe that the speed of the other car is higher than its odometer speed. And if the car is moving away from you, you observe a smaller speed. So, the speed of an object depends on the observer too. But if it is light, according to the second postulate, its speed is independent of the source or the observer.

Actually, the second postulate is against the common sense of what we observe in every day life. It is because, the speed of ordinary objects are very small compared to the speed of light, so we do not realize the relativity in everyday life. The theory of relativity solved some previously unanswered questions in electromagnetic theory.

Simultaneity

One of the results of the special relativity is that time is not an absolute quantity. For example, two events that are simultaneous for one observer may not be simultaneous for another observer.To understand this let us consider the following thought experiment.

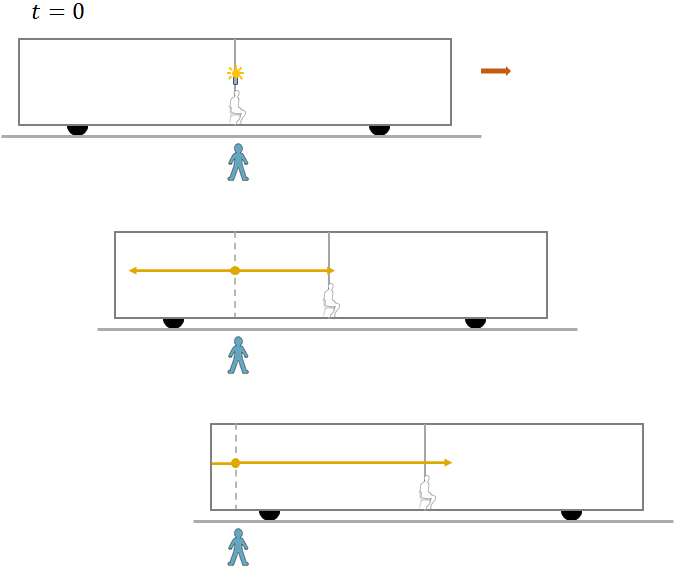
Assume, there is a train moving at some velocity to the right and a person is sitting in the middle of the train. And, another person is standing outside the train, on the platform. The train is approaching the platform and when the two persons just pass each other, a flash of light is given off at the center of the train. The person sitting in the train is observing how long it will take the light to reach the front and the back end of the train. Since the front and the back are equidistant from the center of the train, the light takes same amount of time to arrive at the front and at the back. So, for the person in the train, the two events, the light arriving at the front and the light arriving at the back occur simultaneously.

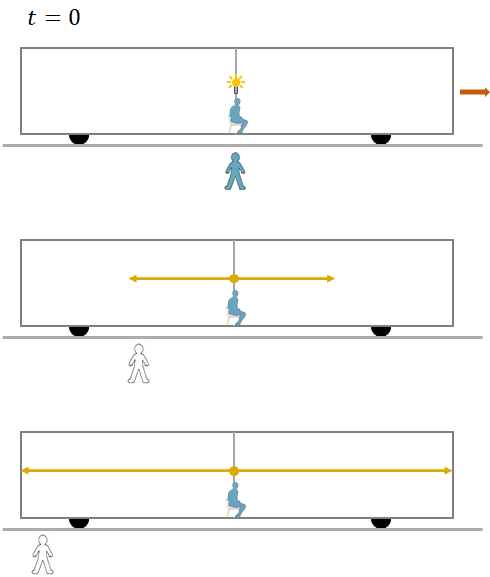
simultaneity observer in train — Observer in the train. A flash of light is given off at t =0.

But for the person on the platform, the back end of the train and the light both are moving toward each other. And, the front end is moving away from the light and the light is chasing it. So, the light arrives at the back earlier than at the front. So, for the person on the ground, the two events are not simultaneous.

simultaneity observer in platform — Observer on the platform. A flash of light is given off at t =0.

Time dilation

Let us consider a spaceship traveling past the earth at a speed $v$. In the spaceship, there is a laser, a mirror, a light receiver and a clock. Let the distance between the mirror and the receiver is d. Now, a person in the spaceship turns on the laser and the light from the laser hits the mirror and reflects back to the receiver.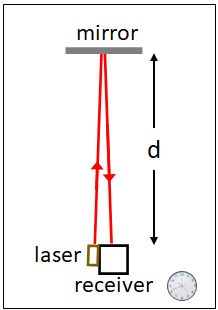

For the observer on the spacecraft, the light travels a distance of 2d, before reaching the receiver. If $\Delta t_0$ is the time, the light takes to travel from the laser to the receiver, then

$\Delta t_0=\dfrac{2d}{c}$.

This is the time, the observer in the spaceship measures with his/her clock.

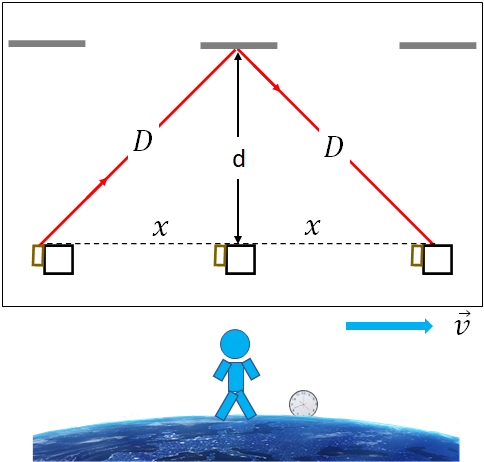
Now, consider, there is a person on the earth watching this experiment. But he/she sees a different path for the light as the spaceship and everything in there is moving. For him/her, the light travels the diagonal paths as shown in the figure above. It travels a distance $D$ from the laser to the mirror and another $D$ from the mirror to the laser. So, the total distance traveled by the light is $2D$. If $\Delta t$ is the time taken by the light to travel from the laser to the mirror and to the receiver, then

$\Delta t=\dfrac{2D}{c}$

This is the time, the observer on the earth measures in his/her clock.

Considering, the distance traveled by the spaceship during the time $\Delta t$ as $2x$, we have

$2x=v \Delta t$

Next step is relating the two times, $\Delta t_0$ and $\Delta t$.

From the geometry of the figure (taking one of the right angled triangle), using the Pythagorean theorem, we can write

$d=\sqrt{D^2-x^2}$

Substituting $D$ and $x$ from the above equations, we get

$d=\sqrt{\dfrac{c^2\Delta t^2}{4}-\dfrac{v^2\Delta t^2}{4}}$

$d=\dfrac{\Delta t}{2}\sqrt{c^2-v^2}$

Substituting $d$ from the very first equation,

$\dfrac{c\Delta t_0}{2}=\dfrac{\Delta t}{2}\sqrt{c^2-v^2}$

Solving for $\Delta t$,

$\Delta t=\dfrac{\Delta t_0}{\sqrt{1-\dfrac{v^2}{c^2}}}$

To write the above equation in a compact form, we take,

$\dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}=\gamma$

Therefore,

$\Delta t=\gamma \Delta t_0$

When $v=0$, $\gamma = 1$.

For any non-zero velocity, $\gamma>1$, and $\Delta t>\Delta t_0$.

So the time interval between two events (here it is sending and receiving light) is greater for the observer on earth than for the observer on the moving spaceship. In other words, a moving clock runs slower than a clock that is in rest. This is known as time dilation.

Time dilation is noticeable only if the speed, $v$ is close to the speed of light. At the ordinary slow speeds, such as the speed of a car, or an airplane, the value of $\gamma$ is close to 1, so the time you measure in a car or in an airplane is same as the time that you measure in the ground. So, time dilation is not noticeable at ordinary speeds.

Proper time

The time interval, $\Delta t_0$ is called proper time. When using the time dilation equation, you may be confused, which one is the proper time and which is not. Proper time is the time interval measured with a clock that is present in the place where both the events take place. In sending and receiving of light that we discussed above, sending is the first event and receiving is the second event. The clock in the spaceship was present in the place where both the events took place, so this clock measures the proper time.

Space travel

The kinematic equations that you learned in physics 1 come under the classical physics or non-relativity. Based on these equations, if you want to travel from Earth to reach a distant object, such as a star that is at a distance of 100 light years from the earth, it will take about 100 years to reach the star. But according to the theory of relativity, if we travel at a speed of $0.999c$, it will take less than 5 years. The only problem is to achieve such a high speed.

GPS navigation system and relativity

Global positioning system or GPS, uses radio signals and satellites to find the location on or near the earth. There is a network of about 30 satellites revolve around the earth at an altitude of about 20200 km from the Earth's surface with an orbital period of about 12 hours. The satellites are placed in orbits such that at least four satellites are visible from any point on earth in a given time. Each satellite has an atomic clock with an accuracy of 1 nano second and with that they send out precisely timed radio signals. The GPS instrument that receives the signals compares the time difference between the signals and determines the position on the earth. Since the satellites are in motion, their clocks run slower than the Earth's bound clocks, according to the special theory of relativity. Calculation shows that a clock on a satellite falls behind a clock on the earth by 7 microseconds per day. This results in a time delay in receiving the signals from different satellites by the GPS, which leads to position inaccuracy. So, all the GPS systems take into account the time dilation and correct the time accordingly so that we can have an accurate GPS.

Length contraction

Assume that there is a spacecraft travels from Earth to another planet, at a speed, $v$. Considering, $\ell_0$ is the distance between the Earth and the planet, the time to arrive the planet is

$\Delta t=\dfrac{\ell_0}{v}$.

This is the time required based on an observer on the Earth. Note that this time is not the proper time as the Earth bound clock is not present at the places where the events (the departure and the arrival) take place.

But for an observer on the spacecraft, the time is shorter due to the time dilation, as the moving clock runs slower. The time as measured by the observer on the spacecraft according to time dilation is

$\Delta t_0=\dfrac{\Delta t}{\gamma}$.

Substituting, $\Delta t$ from the previous equation,

$\Delta t_0=\dfrac{\ell_0}{v\gamma}$.

Now, calculating the travel distance, $\ell$ as observed by the person in the spaceship with the time $\Delta t_0$,

$\ell=v\Delta t_0$

Substituting, $\Delta t_0$,

$\ell=v\dfrac{\ell_0}{v\gamma}$

$\ell=\ell_0/\gamma$.

Since $\gamma\gt 1$, $\ell\lt\ell_0$.

The above equation tells us that the distance shortens with speed. This not only applies to distances but to the length of objects too. So, the above equation tells us that the length of a moving object is measured to be shorter than its length measured when the object is in rest. This is called length contraction.

It is important to note that the length contracts only in the direction of motion of the object. And, there will be no change in dimension of the object that is perpendicular to the direction of motion.

Proper length

The length $\ell_0$ is called proper length. Proper length is the length measured by an observer who is in rest relative to the object. For example, if a person measuring the length of a table with a ruler, then that measurement is the proper length as there is no relative motion between the person and the table.

Time as a fourth dimension

You saw that at very high speeds called relativistic speeds, for an observer who is not moving with the object, length of the object shortens and the object gains time. Length is a dimension. Other dimensions are width and height and these can also change depends on the direction of motion of the object. So, time behaves like one of the dimension as it changes with speed like a dimension of an object. This brought to the idea of adding the time as the fourth dimension, and we have a four dimensional space-time.

Relativistic momentum

You have learned that the magnitude of the momentum of an object moving with velocity $v$ is

$p=mv$

This equation is valid only if the speed of the object is very small compared to the speed of light. When an object is moving at a relativistic speed, we need to use the following equation to find the momentum of the object:

$p=\gamma mv$.

Note that, if the speed of the object is much smaller compared to the speed of light, then the above equation reduces to the regular momentum equation. So, the relativistic momentum equation is valid for all the velocities.

The ultimate speed

Another important result of the special theory of relativity is that the speed of light is the ultimate speed. No object can travel with a speed equal or greater than the speed of light in vacuum. i.e., all objects must travel with a speed less than the speed of light.

Relativistic kinetic energy

You learned that the kinetic energy of an object moving at velocity $v$ is

$KE=\dfrac{1}{2}mv^2$

Like the momentum, this equation is also valid only at smaller speeds. At relativistic speeds, kinetic energy of the object is

$KE=(\gamma-1)mc^2$.

This kinetic energy equation is valid for all velocities.

Mass energy equivalence

We can rewrite the relativistic kinetic energy equation as

$KE=\gamma mc^2-mc^2$.

There are two terms on the right hand side, the second term is called the rest energy of the object as it is independent of the velocity of the object. If you add the rest energy to the kinetic energy of the object, you will get the total energy of the object (assuming the object has no potential energy).

i.e., the total energy of the object is

$E=KE + mc^2$

If the object is in rest, then $KE=0$ and we have

$E=mc^2$.

This is the famous Einstein’s equation.

Addition of relativistic velocities

When objects move towards or away from each other with relativistic speeds, i.e., at speed close to the speed of light, then the simple rule of addition or subtraction of velocities does not work. Assume that there is a spaceship moving away from the earth at a speed, $v$ relative to the earth. Now, if the spaceship fires a rocket at a speed, $u'$, with respect to the spaceship in the same direction as the spaceship's motion, then the speed of the rocket with the earth, $u$, according to the special theory of relativity is

$u=\dfrac{v+u'}{1+\dfrac{vu'}{c^2}}$.

If the rocket is moving opposite to the direction of the spaceship, then $u'$ should be replace with $-u'$.