Magnetism

If you break a magnet into smaller pieces each piece acts as a magnet having a north and a south pole. You cannot have an isolated north or a south pole. i.e., there is no magnetic monopole exists.

Magnetic field

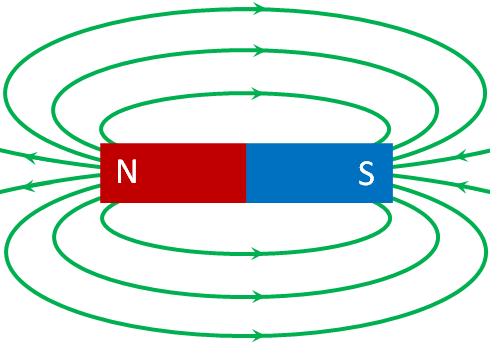
Magnetic field is stronger near the poles, where the magnetic field lines are closer to each other.

Electric currents and magnetic field

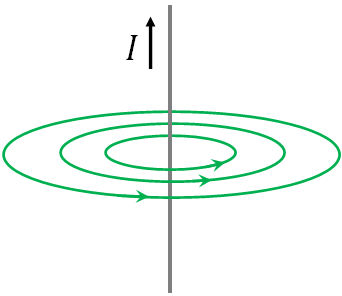
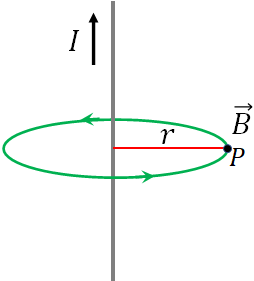
$B=\dfrac{\mu_0 I}{2\pi r}$

The above equation is called Biot-Savart law.

Direction of the magnetic field is determined by the right hand rule: grasp the wire with your right hand so that your thumb points in the direction of the current, then your fingers will curl around the wire in the direction of the magnetic field.

In the figure, the current carrying wire is on the plane of the page. At the point $P$, the direction of the magnetic field is into the page by applying the right hand rule.

SI unit of magnetic field is tesla, $T$ that is same as $N/A.m$.

Force on an electric current in a magnetic field

$F=I\ell B\sin\theta$

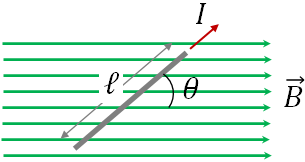
In the figure above, you can find that the direction of the magnetic force on the wire is into the page by the right hand rule.

A moving charge in a magnetic field

When a current carrying wire is placed in a magnetic field, the magnitude of the force, $F$ on the wire by the magnetic field, $B$ is

$F=I\ell B\sin\theta$

If in a time interval, $t$, there is a charge $q$ pass by a given region of the wire, then the magnitude of the current is

$I=q/t$

Substituting this in the force equation:

$F=(q/t)\ell\, B\sin\theta$

$v=\ell/t$

Solving for $\ell$,

$\ell=vt$

$F=qvB\sin\theta$

The direction of the magnetic force on a charge is given by another right hand rule: first stretch your fingers in the direction of the particle's velocity, then curl your fingers in the direction of the magnetic field, now your thumb points in the direction of the force if the charge is positive, or in the opposite direction to the thumb if the charge is negative.

If you substitute, $v=0$ in the above equation, you get $F=0$. That is the magnetic force on a charged particle is zero, when the charge is in rest. Also when, $\theta=0$, $\sin \theta=0$ and you will get $F=0$. That is the force is zero, when the charged particle is moving parallel to the magnetic field. The force is maximum when the direction of motion (or velocity) of the particle and the magnetic field are perpendicular to each other, because in this case $\theta=90^\circ$ and $\sin 90=1$, the maximum value of sine.

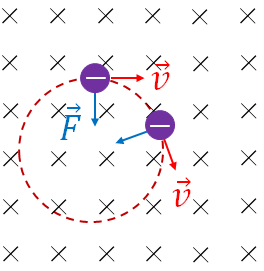
If a charged particle moves perpendicular to a uniform (constant in magnitude and in direction) magnetic field, then the path of the charged particle will be a circle. Since the charge is in circular motion, it has a centripetal force:

$F_c=\dfrac{mv^2}{r}$

The centripetal force is the net force on the charge. If the magnetic force is the only force acting on the charge, then the net force is the magnetic force and we have

$qvB\sin\theta=\dfrac{mv^2}{r}$

$qvB=\dfrac{mv^2}{r}$

$r=\dfrac{mv}{qB}$

Force between two parallel wires

$F=\dfrac{\mu_0 I_1I_2\ell}{2\pi d}$

where $I_1$ and $I_2$ are the magnitude of the currents in the wires, $d$ is the distance between the wires and $\ell$ is the length of the wire (s).

The wire 1 exerts a force on wire 2, which is $\vec F_{21}$ and the wire 2 exerts a force on the wire 1, $\vec F_{12}$. The forces are equal and opposite according to Newton's third law. You can find the magnitudes of the forces by the equation above.

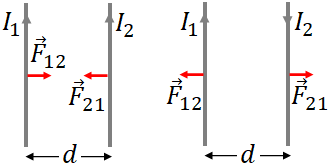
If the currents are in the same direction, then you can see that the two wires attract each other. So, the forces, $\vec F_{21}$ and $\vec F_{12}$ are toward each other. But if the currents are in the opposite directions, then the force is repulsive and the wires push each other away. So, $\vec F_{21}$ and $\vec F_{12}$ are away from each other.

Solenoids

$B=\dfrac{\mu_0NI}{\ell}$

Electromagnet

If a piece of iron is placed inside a solenoid, the iron becomes a magnet. So, the resulting magnetic field inside the solenoid is now the sum of the magnetic field due to the current and that due to the magnet. The result is the magnetic field inside the solenoid increases tremendously, by several hundreds or thousands of time. A solenoid with an iron core is called an electromagnet. Electromagnets have lots of applications. They are used in electric circuit breakers, in door bells, in loudspeakers and in induction heating to name a few.

Ampere's law

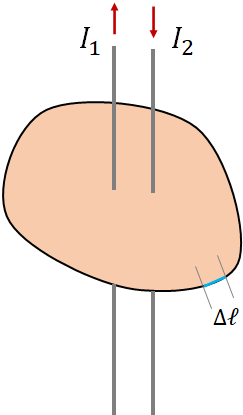
Suppose you have some current carrying wires and you are taking a closed path around the currents as shown in the figure. At any point around a current, there is a magnetic field. Now, split the path into small segments of length Δℓ and find the component of the magnetic field parallel to each of the segments, which is B_||. Now, multiply the B_|| with Δℓ for each segment and add all of them. This sum is equal to $\mu_0$ times the net current enclosed by the closed path. This is what is Ampere's law. i.e.,

$\Sigma B_\parallel \Delta \ell=\mu_0 I_{encl}$

where $I_{encl}$ is the net current passing through the surface enclosed by the path.

Ampere's law is equivalent to the Gauss's law in electrostatics. It is very useful to find the magnetic field of current carrying wires of any shape (not only straight wires). We can also find the magnetic field inside a solenoid by using Ampere's law.

Torque on a current loop

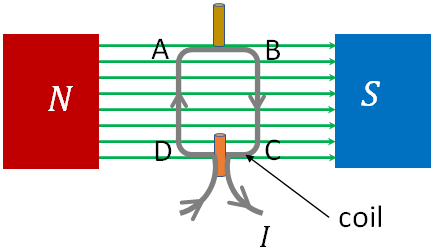
$F=I\ell B\sin 90=I\ell B$

where $\ell $ is the length of the side AD.

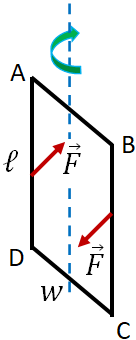
$\tau=\dfrac{w}{2}\,F+\dfrac{w}{2}\,F=wF$

Substituting, $F$ in the equation, we get

$\tau=wI\ell B$

The product of $w$ and $\ell$ is just the area of the coil (rectangle), $A$. So, substituting, $w\ell=A$,

$\tau=IAB$

If the coil has more than one turns, then torque on each coil will add up. So if there are $N$ turns in the coil, then the torque on the coil is

$\tau=NIAB$

Mass spectrometer

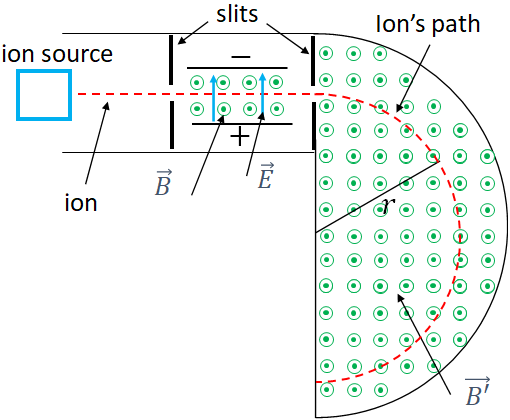
$F_1=qE$,  where $q$ is the charge on the ion.

$F_2=qvB$,  where $v$ is the velocity of the ion.

So, there are two forces on an ion, an upward electric force and a downward magnetic force. Only the ions with certain speed can have the two forces balance, and those ions travel straight and pass through a second slit. All other ions will be deflected above or below the horizontal direction and are blocked by the slit.

Equating the electric and the magnetic forces,

$qE=qvB$

Solving for $v$,

$v=\dfrac{E}{B}$

Only the ions with this speed can pass through the second slit.

The region after the second slit is filled with a magnetic field, $\vec B'$,which is also directed out of the page. The positive ions entering this region are exerted by a magnetic force by the magnetic field. Since the ions travel perpendicular to the magnetic field, they follow a circular path in the clockwise direction. For an ion in circular motion, the magnetic force is the centripetal force as the magnetic force makes the ion to follow the circle, therefore

$qvB'=\dfrac{mv^2}{r}$

Dividing out $v$,

$qB'=\dfrac{mv}{r}$

Substituting $v=E/B$, from the previous equation and solving for $m$, we get

$m=\dfrac{qBB'r}{E}$

For a constant electric and magnetic field, mass of an ion depends on the radius, $r$ of the circular path of the ion. So, by measuring the $r$, we can find the mass of the ion.