Electric potential

Work by electric field

In physics 1, you learned that forces such as push, pull, gravity or friction do work on objects. Like that, an electric force can do work on electric charges.

Let us consider a uniform electric field, $\vec E$ points to the right as shown in the figure below. Assume a positive charge, $q$ is released at point A. Due to the electric field, the charge experiences a force, $\vec F=q \vec E$. And the charge will move in the direction of the force. Since the charge is positive, the direction of the force is in the direction of the electric field. So, the charge moves in the direction of the electric field.

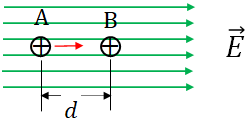
If the charge moves from the point A to another point B, then the work done on the charge by the electric field (i.e., by the electric force) is

$W=Fd\cos\theta$

where$F$ is the magnitude of the force, $d$ is the magnitude of the displacement of the charge between A and B, and $\theta$ is the angle between the force and the displacement. Since the charge moves in the direction of the force, $\theta =0$ and $\cos\theta=1$.

Substituting the magnitude of the force, $F=qE$,

$W=qEd$

This is the work on a positive charge by the electric field. Note that $q$ and $E$ are the magnitudes of the charge and the electric field.

If the charge is negative, then the force on the charge and the electric field are in the opposite directions. So, the charge will move in the opposite direction to the electric field.

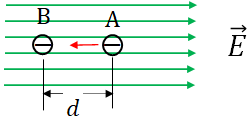
work on a negative charge by an electric field

But still the charge move in the direction of the force, so the work will be the same. So, the work done on any type of charge by an electric field is

$W=qEd$

Note that in deriving this equation, we consider only the force by the electric field on the charge. If there are other forces acting on the object, then you need to add the work by those forces in the above equation.

Work and change in potential energy of a charge

When a work is done on an object by a conservative force, the potential energy of the object changes. An electric force is a conservative force. So, when a work is done on a charge by an electric force, the potential energy of the charge changes according to,

$W=-\Delta PE$

where $W$ is the work done on the charge by the electric force and $\Delta PE$ is the change in potential energy of the charge.

So, when the charge moves from A to B,

$W=-(PE_B-PE_A)$

where $PE_A$ and $PE_B$ are the electric potential energy of the charge at point A and point B respectively.

Substituting, $W=qEd$, and solving for $PE_B$, we get

$PE_B=PE_A-qEd$

This equation shows that when a work is done on a charge by an electric field decreases the potential energy of the charge.

Electric potential

Potential energy of a charge in an electric field depends on the charge as well as its position (A or B), which you can see in the equation above. Now, we are going to define a quantity that is independent of the charge but depends on the position of the charge, such as the points A and B. Such a quantity is called electric potential.

Electric potential, $V$ at a point is defined as the electric potential energy, a charge possesses at the point divided by the charge:

$V=\dfrac{PE}{q}$

So, the change in electric potential, $\Delta V$ from the point A to the point B is

$\Delta V=V_B-V_A$

where $V_A$ and $V_B$ are the electric potentials at the points A and B respectively.

Substituting, $V=\dfrac{PE}{q}$

$\Delta V=\dfrac{PE_B-PE_A}{q}$

$=\dfrac{\Delta PE}{q}$

$\boxed{\Delta PE = q\Delta V}$

This equation tells us that how much the potential energy of a charge changes when it moves from one point to another with a change in potential of $\Delta V$.

Now putting $W=-\Delta PE$, in this equation, we get,

$\boxed{W=-q\Delta V}$

This equation tells us how much work needs to be done to move a charge, $q$ from one point to another with a change in potential of $\Delta V$.

Now, putting $W=qEd$, in the above equation, and solving for $E$, we get

$\boxed{E=-\dfrac{\Delta V}{d}}$

This equation relates the electric field and the change in electric potential between two points and the distance between the points.

The magnitude of the change in electric potential between any two points is called the electric potential difference.Electric potential difference is also called voltage. SI unit of electric potential difference or electric potential is volt (V).

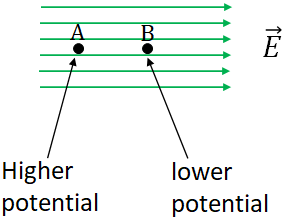
From the above equation, you can see that the direction of the electric field is from the higher potential to the lower potential.

Equipotential lines and surfaces

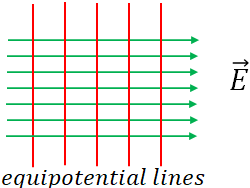
Equipotential lines or equipotential surfaces refer to the lines or surfaces on which all the points are at same electric potential. That is $V$ is constant on an equipotential line or on an equipotential surface. So, the potential difference, $\Delta V$ between any two points on an equipotential line or an equipotential surface is zero.

To move a charge from one point to another, the work required is $W=-q\Delta V$. Since $\Delta V=0$ on an equipotential surface, no work is required to move a charge from one point to another on an equipotential line or surface.

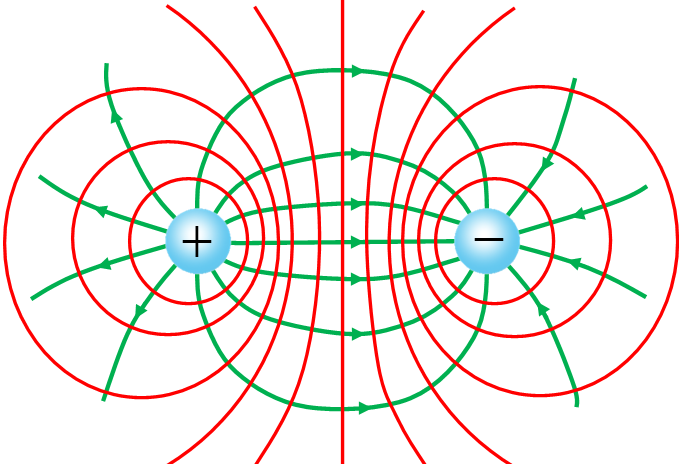
The electric field lines and the equipotential lines (or surfaces) are perpendicular to each other. So it is easy to draw the equipotential lines (or surfaces) when the electric filed lines are known.

The equipotential lines (red lines) for a uniform electric field is shown below. At any point in the field, the equipotential line is perpendicular to the electric field.

In the figure below, the equipotential lines (red lines) around two charges of opposite signs with same magnitude are shown.

The electron volt

SI unit of energy is joule but it is a very large unit if you are dealing with energies of electric charges, so we define a smaller unit called electron volt.

One electron volt is defined as the energy acquired by a particle of charge, $e$, when moving through a potential difference of $1 V$ (think about the equation, $\Delta PE =q\Delta V$). The conversion factor from $eV$ to $J$ is

$1eV=1.602\times 10^{-19}J$

Electric potential due to a point charge

If you have a point charge, what is the electric potential at a point near the charge?. This you can find by using calculus.

The electric potential, V at a distance $r$ from a point charge $q$ is

$V=k\dfrac{q}{r}$

In this equation, if you put $r=\infty$, you get V=0. That is at an infinite distance from a charge, the electric potential is zero.

Note that electric potential is a scalar. Therefore, it is easy to work with electric potential than electric field, which is a vector. If you know the electric potential, you can find the electric field from that. When using the above equation, you need to include the sign of the charge.

Capacitors

A capacitor is an electric device that consists of two conducting plates or sheets placed close to each other without touching. There are different types of capacitors. Parallel plate capacitors are more common. We can use capacitors to store electric charge and electric energy.

A parallel plate capacitor consists of two parallel plates of area $A$, separated by a distance $d$. When a battery is connected to the capacitor, one of the plates acquires negative charge and the other an equal amount of positive charge (You will learn more about this later).

In any capacitor, the amount of charge on each plate is proportional to the magnitude of the potential difference or voltage, $V$ between the plates:

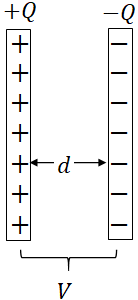
$Q=CV$

where the proportionality constant, $C$ is called the capacitance of the capacitor. Note that, here I used V instead of ΔV for the potential difference.

Capacitance depends on the size and shape of the capacitor but it is independent of $Q$ or $V$ as $Q$ and $V$ are proportional. Unit of capacitance is coulomb per volt, that is called farad, (F).

Capacitance of a parallel plate capacitor

In electric field, you learned that the electric field between two conducting charged parallel plate is

$E=\dfrac{\sigma}{\epsilon_0}$

And, we have the equation

$E=-\dfrac{\Delta V}{d}$

If the voltage (or the potential difference) between the two plates of the capacitor is V, and just take the magnitude of the electric field (ignoring the sign), then we get

$E=\dfrac{V}{d}$

where $d$ is the distance between the plates, i.e., the plates separation.

Putting E, from the first equation,

$\dfrac{\sigma}{\epsilon_0}=\dfrac{V}{d}$

If the charge on one of the plate is $Q$, and $A$ is the area of each plate, then the surface charge density of a plate is $\sigma = Q/A$, so we get

$\dfrac{Q\sigma}{A\epsilon_0}=\dfrac{V}{d}$

$\dfrac{Q}{V}=\epsilon_0 \dfrac{A}{d}$

Left hand side is nothing but the capacitance, $C$. Therefore, the capacitance of a parallel plate capacitor is

$C=\epsilon_0 \dfrac{A}{d}$

From this equation, you see that larger the area of the plates, larger the capacitance value. Also, smaller the plates separation, larger the capacitance.

Dielectrics

In most capacitors, there is an insulating sheet of material, such as a piece of paper or plastic is placed between the plates. The insulating materials are called dielectrics. The dielectric increases the capacitance of the capacitor.

The capacitance of a capacitor with a dielectric inserted between the plates is

$C=K\epsilon_0 \dfrac{A}{d}$

where $K$ is called the dielectric constant of the dielectric or the insulating material.

If there is no material inserted between the plates of a capacitor, then what is in there is air. For air $K=1$. Inserting a dielectric material increases the capacitance by a factor of $K$. The dielectric constant of paper is $3.7$. So, placing a sheet of paper between the plates of a capacitor increases the capacitance by $3.7$ times.

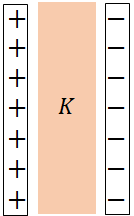
a parallel plate capacitor with a dielectric

A dielectric placed between the plates of a capacitor decreases the electric field and hence the potential difference between the plates, which in turn increases the capacitance. The dielectric does not affect the charge of a capacitor but it reduces the voltage between the plates so the capacitance of the capacitor increases.

Energy stored in a capacitor

To charge a capacitor a work needs to be done on the capacitor. That work move the charge from one plate to the other. The work is done by the battery that charges the capacitor. This work is stored as the electric potential energy of the capacitor. By using calculus, we can find the stored electric potential energy of a capacitor:

$PE=\dfrac{1}{2}QV$

From, $C=Q/V$, we have $Q=CV$. Substituting this in the above equation, we have

$PE=\dfrac{1}{2}CV^2$

Energy stored in an electric field

We found that the energy stored in a capacitor is

$PE=\dfrac{1}{2}CV^2$

If we consider a parallel plate capacitor, the electric field between the plates is constant and is related to the potential difference between the plates by the following equation,

$V=Ed$ where $d$ is the plates separation.

This is the absolute value of the potential difference between the plates.

Also, the capacitance of a parallel plate capacitor is

$C=\epsilon_0 \dfrac{A}{d}$

Substituting $V$ and $C$ in the PE equation,

$PE=\dfrac{1}{2}\epsilon_0 \dfrac{A}{d}E^2d^2$

$=\dfrac{1}{2}\epsilon_0 (Ad)E^2$

The product, $Ad$ is nothing but the volume, $V$ of the space between the plates. Substituting $Ad=V$,

$PE=\dfrac{1}{2}\epsilon_0 VE^2$

Dividing both sides by $V$, we get

$\dfrac{PE}{V}=\dfrac{1}{2}\epsilon_0 E^2$

The ratio on the left hand side is the energy per unit volume, which is called the energy density, $u$. So,

$u=\dfrac{1}{2}\epsilon_0 E^2$

This equation shows that the energy density of a capacitor depends only on the electric field. From this, we can conclude that, in a capacitor, the energy is stored in the electric field between the plates of the capacitor. Alternately, we can say that if there is an electric field $E$, there is an energy stored in it with energy density given by the above equation.