Early quantum theory and early models of the atom
Discovery of electron
It was found around 1870 that when a high voltage (~100 kV) is applied between two metal plates placed inside a vacuum glass tube, one end of the glass tube began to glow as shown in the figure below. The metal plates are called electrodes. The electrode, where the positive terminal of the DC power source is connected is called anode and the electrode where the negative terminal is connected is called cathode. The glow was behind the anode on the glass wall. Along with the glow, there was a shadow of the cross shaped anode on the glass wall. So, it was realized that something was traveling in straight lines from the cathode. Since it was coming from the cathode, it was named cathode rays. These cathode rays are invisible but when it hits the glass, the glass molecules are excited and release light, which results in the glow.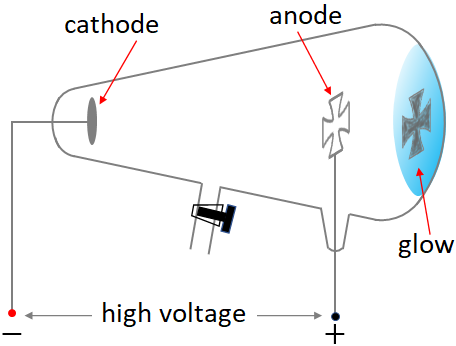
In the same year, J. S. Townsend first measured the charge, $e$ of an electron. But the more accurate value of, $e$, was obtained by Robert Millikan in 1909 with his famous experiment called Millikan’s oil drop experiment. From the value of Thomson’s $e/m_e$ and the value of $e$, the mass of the electron, $m_e$, was determined.
Blackbody radiation
All objects absorb and emit radiation to some degree. If an object absorbs all the radiation falling on it, then we call that a blackbody. A blackbody is an ideal object, which not only absorb the radiation but it can also emit radiation. A blackbody emits radiation if its temperature is greater than 0K. The radiation is produced by the vibrations (oscillations) of atoms or molecules of the blackbody. i.e., when atoms or molecules oscillate, the charge of them oscillate, and the oscillating charges produce electromagnetic (EM) waves or radiation. We can approximate most of the ordinary objects as a blackbody.The total intensity, $I$ of radiation emitted by an object depends on the temperature. It is proportional to the fourth power of the absolute temperature as you learned in the topics on heat.
i.e., $I\propto T^4$.
At low temperature, around 300K (room temperature), the intensity of radiation is very small, therefore we cannot feel or see the radiation.
At higher temperatures but lower than 1000K, objects emit infrared radiation. The radiation can be felt near the object.
At temperatures above 1000K, objects glow. Examples: red-hot burner of an electric stove and heating element of a toaster.
At temperatures above 2000K, objects glow with yellow or whitish color. Example: filament of an incandescent light bulb.
Blackbody spectrum
The radiation emitted by an object (blackbody) contains a continuous range of wavelengths or frequencies. If we plot a graph of the intensity of radiation versus wavelength (or frequency) we call it a blackbody spectrum, which is given in the figure below.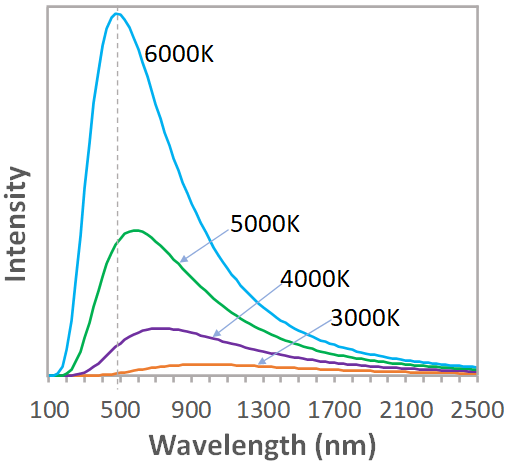
Wien’s law
From the blackbody spectrum, you can see that, as the temperature increases, the peak of the spectrum shifts toward lower wavelengths (or higher frequencies). i.e., at 6000 K, the peak wavelength is about 500nm, but at 5000K, the peak is around 600 nm. The peak wavelength,$\lambda_p$ (in m) of a spectrum is inversely proportional to the absolute temperature,$T$.i.e., $\lambda_p \,T=2.90\times 10^{-3} \:m\,K$.
This equation is called Wien’s law.
Planck’s quantum hypothesis
In the year 1900, Max Planck proposed a theory, known as Planck's quantum hypothesis, by which he was able to reproduce the blackbody spectrum with an equation. His theory is that "Energy of oscillation of an atom or a molecule cannot have just any value, the only possible energy values are an integer multiple of a minimum energy." This minimum or the smallest possible energy is called a quantum of energy.The minimum energy of atomic or molecular oscillation (according to Planck's hypothesis) is $hf$, where $f$ is the frequency of the oscillation and $h$ is a constant called Planck's constant. The value of $h$ is
$h=6.626\times 10^{-34}Js$
So, according to Planck's hypothesis, the energy of oscillation of an atom or a molecule is$E=nhf$
where $n=1,2,3, ...$ is called quantum number.The most notable point is, the energy of atomic or molecular oscillation is not continuous, but is discrete, i.e., the energy can be $hf$, $2hf$, $3hf$, .... and there is no other values in-between. Therefore, we say that the energy of atomic or molecular oscillation is quantized.
The Plank's quantum theory is the beginning of quantum physics.
Einstein photon theory of light
Einstein extended the idea of discreteness of energy of atomic oscillation to the energy of light. In 1905, Einstein proposed a theory that light is emitted and transmitted as tiny particles, called photons. i.e., Einstein photon theory consider light as particles, and the particles are called photons. A photon has energy and momentum but has no mass.Energy of a photon is
$E=hf$
where $f$ is the frequency of the photon (or the light).Momentum of a photon is
$p=\dfrac{h}{\lambda}$
where $\lambda$ is the wavelength of the photon (or the light).Photoelectric effect
When light shines on a metal surface, electrons are emitted from the metal. This emission of electrons induced by light is called photoelectric effect. And the emitted electrons are called photoelectrons. Since light is an electromagnetic wave, the electric field of the light exerts a force on the electron, which ejects the electron from the surface of the metal.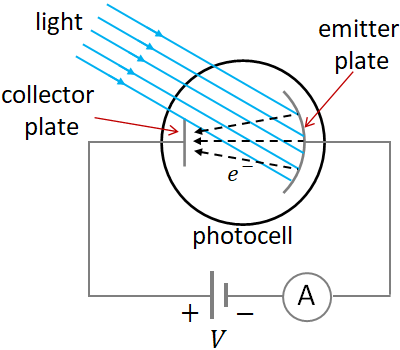
An apparatus used to demonstrate the photoelectric effect is the photocell. A photocell consists of a curved metal plate, called (emitter plate) and a small electrode, called collector plate in an evacuated glass enclosure. A battery and an ammeter (A) are connected in series to the photocell. The positive terminal of the battery is connected to the collector plate and the negative terminal to the emitter plate. So, the collector plate is at higher potential and the emitter plate is at lower potential. When light illuminates the emitter plate, it emits electrons. The emitted electrons move toward the collecting plate as electrons move from lower potential to higher potential. Due to the flow of electrons, a current flows in the circuit that is indicated by the ammeter. When no light incident on the plate, there is no current flows in the circuit.
The photoelectrons are emitted with a range of speeds, so the kinetic energies. The kinetic energy of the fastest moving electrons is known as the maximum kinetic energy. By reversing the polarity of the battery, and adjusting the voltage, we can find the maximum kinetic energy. When the voltage is reversed, i.e., connecting the negative terminal to the collecting plate and the positive terminal to the emitter plate, the collector plate is now at lower potential. So, the photoelectrons experience a repulsive force by the collector plate, which tries to stop the electrons. The repulsive force is proportional to the magnitude of the voltage across the plates. So, a certain voltage can stop the electrons of up to a certain speed. If we increase the voltage from 0 V, at one point there will be no current. At this point we have stopped all the electrons including the fastest moving.The voltage at which all the electrons are just stopped so that no current in the circuit is called the stopping voltage or the stopping potential.
Since the stopping potential is just the correct amount of voltage to stop the fastest moving electrons, we can relate it to the maximum kinetic energy of the electrons. If an electron moving with a kinetic energy, $KE_{max}$ is stopped, then the loss in kinetic energy by the electron is equal to the electric potential energy gained by the electron. At the stopping potential, $V_0$, the energy gained by the electron is $eV_0$, therefore, we have
$KE_{max}=eV_0$
Experiments on photoelectric effect reveal the following facts.
- There is no electrons emitted if the frequency of the light is below a certain frequency, called cutoff frequency.
- If the frequency of the light is above the cutoff frequency, there is always electrons emitted even if the intensity is low.
- If the frequency is above the cutoff frequency, increasing the intensity increases the number of photoelectrons, but it does not change the maximum kinetic energy of the electrons.
Electromagnetic wave theory of photoelectric effect
In the electromagnetic wave theory, light is considered as waves and the waves are the propagation of oscillating electric and magnetic fields. With the wave theory, we can predict the following regarding the photoelectric effect.- Increasing the intensity of the light increases the maximum kinetic energy of the ejected electrons. This is because, increasing the intensity of the light increases the amplitude of the electric field, which makes the electrons on the metals oscillate violently so that they are ejected at higher velocities.
- Frequency of the light does not affect the maximum kinetic energy the electrons.
The above predictions by electromagnetic wave theory is in contrary to what is actually happening. So, we can conclude that the wave theory fails to explain the photoelectric effect.
Einstein theory of photoelectric effect
Einstein proposed a photoelectric theory, called Einstein photon (particle) theory, which correctly predicts all the features of the photoelectric effect. Following are the Einstein's predictions,- It takes one electron to eject one photon, and during the process the photon is fully destroyed. Increasing the intensity of light, increases the number of ejected electrons as increasing the intensity increases the number of photons.
- Electrons in a metal are bound to the metal by a binding energy, which is called work function, $W_0$. If the energy of the photon is less than the work function, then no photoelectrons emitted. So, the minimum energy of photon for photoelectric effect is
$hf_0=W_0$
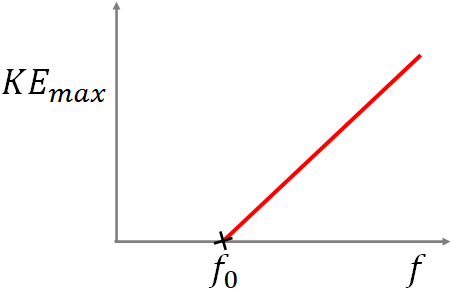
where $f_0$ is the cutoff frequency for the photoelectric effect. If the frequency of the light is greater than the cutoff frequency, then there are electrons emitted. And, above the cutoff frequency, if the frequency is increased, the maximum kinetic energy of the photoelectrons increases according to the following equation:
$KE_{max}=hf-W_0$
A graph of the maximum kinetic energy of photoelectrons vs the frequency of the light (photon) is given below.
Wave-particle duality
In the photoelectric effect, light behaves as particles called photons. But in interference, and diffraction you saw that light behaves as waves. This dual property of light is referred to as the wave-particle duality.Matter waves
Louis de Broglie extended the idea of wave-particle duality of light to other particles or objects. He proposed that if light can behave as waves as well as particles, any particle in motion can also behave like a wave. If we consider particles as waves, we call that waves matter waves. If a particle behave as a wave, it should have a wavelength. Louis de Broglie proposed a formula for the wavelength of matter waves based on the momentum of photons. The wavelength, $\lambda$ of a matter wave is$\lambda=\dfrac{h}{p}$
where $p$ is the momentum of the particle, i.e., $p=mv$, where $m$ and $v$ are the mass and the velocity of the particle. The wavelength of a matter wave is called de Broglie wavelength. Note that we cannot see waves when ordinary object move. This is because the wavelength is very small for those objects.Early models of the atom
In the earlier times, various models of atoms were proposed. Notable models are- Plum pudding model and
- Rutherford planetary model.
Plum pudding model
The plum pudding model was developed in 1904 by J. J. Thomson. This model considered atom as a homogeneous sphere of positive charge with negatively charged electrons embedded in it. That is, electrons are like plums inside a pudding of a positive charge.
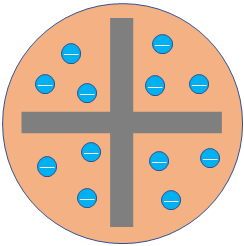
Rutherford planetary model
In 1911, Rutherford performed an experiment with a gold foil. He sent a beam of alpha particles (alpha particles are the positively charged nuclei of helium) into a thin gold foil. Most of the alpha particles pass through the metal. But some of the alpha particles, bounced off into all directions and even some back into the alpha particles source. These are not possible if the plum pudding model is correct. Based on these observations, Rutherford proposed that most of the atom is empty and there is a tiny positively charged core at the center of the atom. That core now we call nucleus. With his findings, Rutherford developed a planetary model of the atom. In this model, nucleus is at the center of the atom, and electrons revolve in orbits around the nucleus. This planetary model was a major step toward the current model of the atom.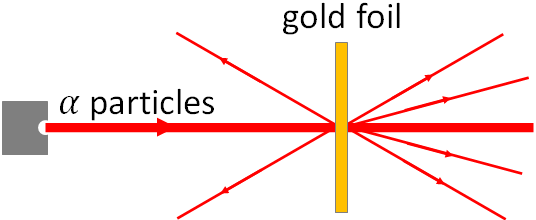
Atomic spectra of gases
When a gas filled tube, known as a discharge tube is applied with a high voltage, the gas emits light. The emitted light is not continuous but is discrete and has only a certain wavelengths. The spectrum of the emitted light is called emission spectrum. An emission spectrum has a series of lines of different wavelengths, so it is called a line spectrum.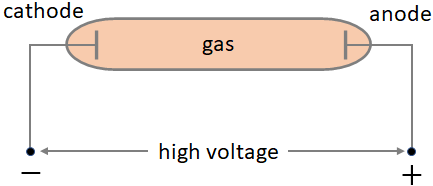
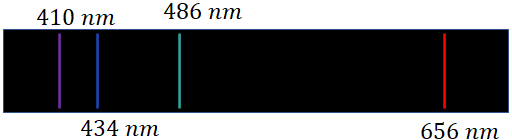
The emission spectrum of the hydrogen gas is given below. There are four lines in the visible region with the wavelengths, 410 nm, 434 nm, 486 nm and 656 nm.
The emission spectrum is unique for a gas, so we can identify a gas by its spectrum.
Further, if we pass white light through a gas, and examine the transmitted light, we will see that certain wavelengths of the light are missing. If we pass the transmitted light through a diffraction grating, you will see the spectrum of the light with dark lines for the missing wavelengths. The light corresponding to the missing wavelengths are absorbed by the gas. The interesting thing is the missing wavelengths correspond to the wavelengths in the emission spectrum. i.e., a gas absorbs and emits light at the same wavelengths (or frequencies).
The hydrogen atom
Hydrogen atom has only one electron orbiting its nucleus. The spectrum of hydrogen in the visible to the infrared region is given below. In the visible region, there are four lines in the spectrum.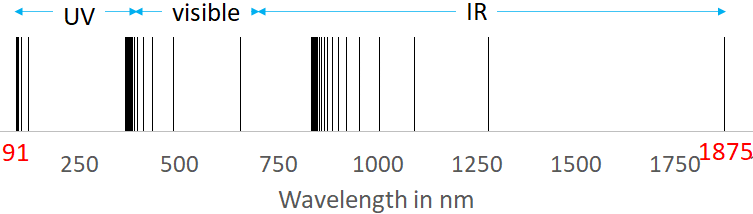
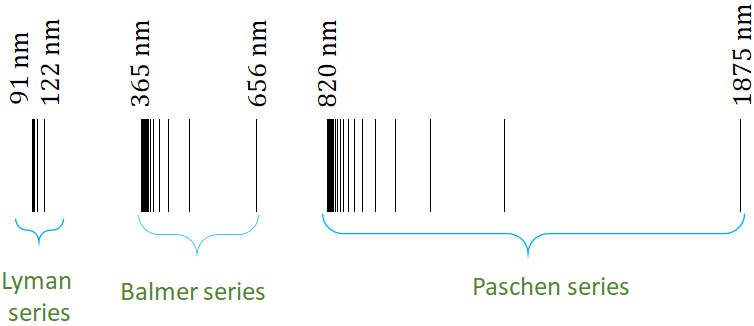
You see that there are three groups of spectral lines, called Lyman series, Balmer series and Paschen series.
These series were named so because, Lyman, Balmer and Paschen found a formula to fit the spectral lines in the UV, visible and the IR spectral lines respectively.
J. J. Balmer in 1885, found a formula to fit the visible spectral lines of the hydrogen atom. Later, his formula was generalized to include other wavelengths in the series that we call Balmer series. The formula for the Balmer series is
$\dfrac{1}{\lambda}=R \bigg (\dfrac{1}{2^2}-\dfrac{1}{n^2}\bigg )$, $n=3,4,5,...$
where $R$ is a constant called, Rydberg constant, $R=1.09737 \times 10^7 m^{-1}$ and $n= 3, 4, 5, .....$. If you put $n=3$, you will get, $\lambda = 656 nm$, and $n=4$, $\lambda = 486 \,nm$, $n=5$, $\lambda = 434 \,nm$ and $n=6$, $\lambda = 410 \,nm$, the wavelength of the four visible lines in the spectrum. The Balmer series covers other spectral lines of wavelength up to 365 nm. The 365 nm corresponds to $n=\infty$.
The Lyman sries covers the spectral lines of wavelength from 91 nm to 122 nm. The formula for the Lyman series is
$\dfrac{1}{\lambda}=R \bigg (\dfrac{1}{1^2}-\dfrac{1}{n^2}\bigg )$, $n=2,3,4,...$
Note that here $n$ starts with 3.The Paschen series of the spectral lines covers wavelength from 820 nm to 1875 nm. The formula for the Paschen series is
$\dfrac{1}{\lambda}=R \bigg (\dfrac{1}{3^2}-\dfrac{1}{n^2}\bigg )$, $n=4,5,6,...$
Note that here $n$ starts with 4.With the Rudherford model, we cannot explain the spectrum of an atom. So, we need another model of the atom. In 1913, Niels Bohr developed a model of the atom. His model was successful in explaining the emission spectrum of the hydrogen atom.
The Bohr model of atom
Bohr developed a model of an atom based on quantum theory. In his model,1. electrons move in circular orbits around the nucleus but only certain orbits are allowed. An electron in each orbit has a definite energy, and when an electron moves in its orbit, it does not radiate energy. Note that, if an object is in circular motion, then it has an acceleration. So, the electron in an orbit has an acceleration. Since an accelerating charge emits radiation, the electron should also emits radiation. If it does, then it loses its energy and finally would collapse into the nucleus, but this doesn't happen. So, Bohr theorized that when an electron revolving around the nucleus in an orbit, it does not radiate energy. The orbits of electrons are called stationary states.
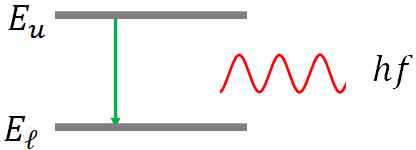
When an electron jumps from a stationary state of higher energy (upper state) to another stationary state of lower energy (lower state), it loses energy. This lost energy is emitted as a photon. The energy of the emitted photon is exactly equal to the energy difference between the two states. That is,
$hf=E_u-E_\ell$
where $hf$ is the energy of the emitted photon and $f$ is the frequency of the photon, and $E_u$ is the energy of the upper state and $E_\ell$ is that of the lower state.2. Angular momentum of an electron in an atom is quantized. That is an electron can have only certain discrete values of angular momentum. According to Bohr, the angular momentum of an electron in an orbit is
$L=n\dfrac{h}{2\pi}$
where $n$ is the orbit’s number, and is called principal quantum number.
Hydrogen atom's orbits
Let us consider the electron of a hydrogen atom is revolving in a circular orbit, $n$ of radius $r_n$.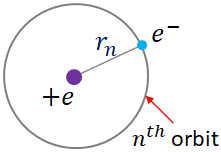
The angular momentum of the electron in the orbit is
$L=mr_nv$
where $m$ is the mass of the electron, and $v$ is the velocity of the electron in the orbit.
From the previous section, we have,
$L=n\dfrac{h}{2\pi}$
From the above two equations, we can find the speed of the electron in an orbit:
$v=\dfrac{nh}{2\pi r_n m}$
Since the nucleus of the atom is positively charged, there is a force of attraction between the nucleus and the electron. The charge of nucleus of the hydrogen atom is $+e$ as there is only one proton in the nucleus. So, the magnitude of the force according to the Coulomb's law is
$F= k \dfrac{e\cdot e}{r_n^2}$
This force keeps the electron in its circular orbit. So, this is the centripetal force on the electron. Therefore,
$\dfrac{mv^2}{r_n}=k \dfrac{e^2}{r_n^2}$
Substituting $v$ from above, and solving for $r_n$, we get
$r_n=\dfrac{n^2h^2}{4 \pi^2 m k e^2}$
Now, substituting the values of $h, m, k$ and $e$, we will get,
$r_n=(0.529 \times 10^{-10})\, n^2$
This is the radius of the nth orbit that is proportional to n2.
For the first orbit, $n=1$, putting $n=1$ in the above equation, you will get the radius of the first orbit:
$r_1=0.529 \times 10^{-10}\, m$
This is the radius of the smallest orbit of the electron.
The radius of the second ($n=2$), orbit is
$r_2=2.12 \times 10^{-10}\, m$
And, for the third orbit (n=3), the radius is
$r_3=4.76 \times 10^{-10}\, m$
Energy of the electron orbits
Now, let us find the energy of the orbits. The energy of an orbit is the total energy of an electron in that orbit. An electron in an orbit has potential energy and kinetic energy.
The potential energy of the electron is
$PE=qV=-eV$
where $V$ is the electric potential at the position of the electron. This electric potential is due to the nucleus of the atom. When the electron is in the nth orbit, it is at a distance of $r_n$ from the nucleus. So, the electric potential due to the nucleus is
$V=\dfrac{kq}{r_n}=\dfrac{ke}{r_n}$.
Substituting this in the above equation, you get,
$PE=-\dfrac{ke^2}{r_n}$
The kinetic energy of the electron is
$KE=\dfrac{1}{2}mv^2$
So, the total energy of the electron in the nth orbit is
$E_n=\dfrac{1}{2}mv^2-\dfrac{ke^2}{r_n}$
Now, substituting, $v$ and $r_n$ from the previous section, and simplifying, we get
$E_n=-\dfrac{2 \pi^2e^4mk^2}{h^2 n^2}$,
Subsitituting the values of the constants, $e$, $m$, $k$ and $h$, we get
$E_n=-\dfrac{13.6 \,eV}{n^2}$, $n=1, 2 , 3, ...$
This is the energy of the nth orbit. To find the energy of the first orbit, put $n=1$, for the second orbit, put $n=2$ and so on.The energy of first orbit is
$E_1=-13.6 \, eV$
This is the energy of the lowest state. This state is called the ground state.
The energy of the second (n=2) and the third (n=3) states are
$E_2= -3.40 \,eV$
and$E_3=-1.51 \,eV$
So the energy is not continuous but is discrete. Because, we have energies, -13.6 eV, -3.40 eV, -1.51 eV,..., and there is no energy in between these values. That is the energy is quantized. Note that the energy is negative. The orbits and the energy of each orbit are shown in the figure below.
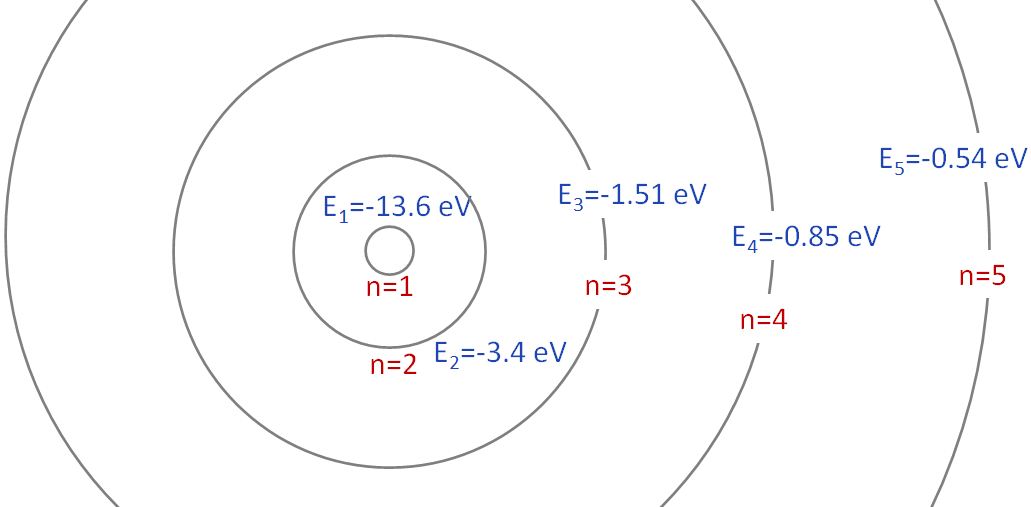
The energy of the orbit (state) increases as we move away from the nucleus. The lowest energy state (n=1), is called the ground state. The higher energy states, $E_2, E_3,....$ are called excited states.
Spectral lines and the Bohr model
Another way to show the states of a hydrogen atom is as shown below. Here, different states (orbits) and the energy of each state are shown.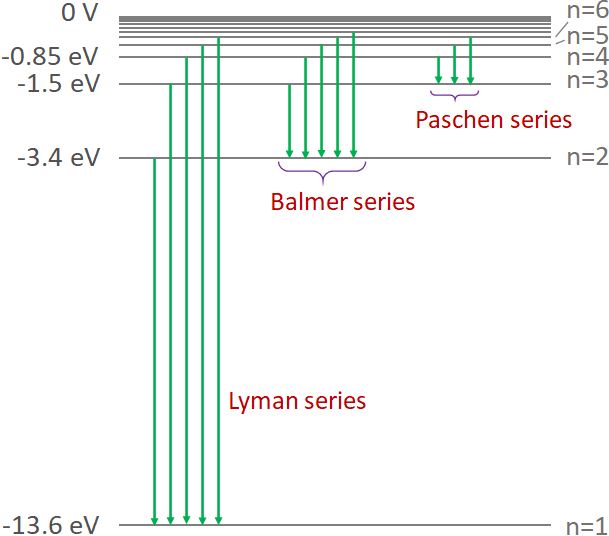
According to the Bohr's model, when an electron jump from a higher energy state to a lower energy state, a photon is emitted. And the energy of the emitted photon is equal to the energy difference between the two states. At normal temperatures, electrons in the atoms of a gas are at the ground state. At higher temperatures or due to the excitation in discharge tubes, many electrons move to the excited states. An electron in an excited state cannot stay there for a long time, so it returns to the ground state. When the electron jump to a lower state, it gives off a photon in the process. Since, the energy of the states are discrete, the spectrum is not continuous instead there are lines and each line corresponds to the energy difference between the two states where the electrons of the atoms made a jump. This is the origin of the emission spectrum of gases.
As shown in the figure, each spectral line in the Lyman series is due to the jumping of electrons from one of the higher state to the ground state (n=1). In Palmer series, each spectral line is the result of electrons jumping from a higher state to the n=2 state. And, each line in the Paschen series is due to the electrons jumping from one of the higher state to the n= 3 state.
Now, let us consider an electron make a transition from a state n to a lower state n'. During this process a photon is released. The energy of the emitted photon is
$hf=E_n-E_{n'}$
We have, $E_n=-\dfrac{2 \pi^2e^4mk^2}{h^2 n^2}$
Substituting, $f=c/\lambda$ and $E_n$ and $E_{n'}$ from the above equation, we get
$\dfrac{hc}{\lambda}=-\dfrac{2 \pi^2e^4mk^2}{h^2 n^2}+\dfrac{2 \pi^2e^4mk^2}{h^2 n'^2}$
From this, we can write,
$\dfrac{1}{\lambda}=\dfrac{2 \pi^2e^4mk^2}{h^3c}\bigg(\dfrac{1}{n'^2}-\dfrac{1}{n^2}\bigg)$
Now, substituting the constants, we get
$\dfrac{1}{\lambda}=R\bigg(\dfrac{1}{n'^2}-\dfrac{1}{n^2}\bigg)$
This equation is of the same form as the formula we used for the Lyman, Balmer or the Paschen series with n'=1 corresponds to the Lyman series, n'=2, the Balmer series and n'=3, the Paschen series. So, with the Bohr theory we have derived those formulae. Thus the Bohr model of atom is successful in explaining the spectrum of hydrogen atom.
