Rotational motion
Rotational motion is the motion of an object rotating about a fixed axis. Some of the examples of rotational motion are the Earth's rotation about its axis, a rotating merry-go-round and the rotating wheels of a car. Circular motion is a special type of rotational motion.In kinematics, you studied 1 and 2-D motion of objects, where objects move from one place to another. Now, we will call that motion, translational or linear motion to distinguish it from the rotational motion.
Rotating rigid body
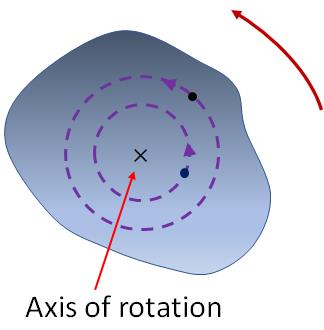
When studying the rotational motion of objects, we consider the objects as rigid bodies. What is a rigid body?. A rigid body is a solid object, where the distance between any two points in the object is constant. Any external force acting on a rigid body does not deform the object so that the distance between any two points remains the same. But, in reality, there is no ideal rigid body exists as all objects undergo deformation when a force is applied on them. In most cases, the deformation is so small, we can ignore them and consider the objects as rigid bodies.In the figure below, a rotating rigid body is shown. To study the rotational motion of the rigid body, we consider it as a collection of large number of small objects, called point objects. When the rigid body rotates, all the point objects rotate about an invisible line, called the axis of rotation of the body. So, the point objects are in circular motion on different circles. For a point object, the radius of the circle is the distance of it from the axis of rotation. In the figure, the circular motion of two point objects are shown. Point objects closer to the axis of rotation moves slower than those far away from it. For example, in a merry-go-round, a person sitting farther from the center (through which the axis of rotation passes) moves faster than the one closer to it.
Angular displacement
Angular displacement of an object is how much angle, the object has rotated and in what direction. The direction can be clockwise, counterclockwise or something else.Definition of angular displacement
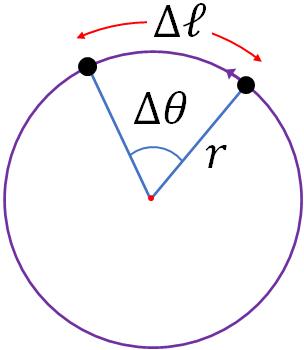
Consider a point object in a rigid body that is at a distance $r$ from the axis of rotation of the rigid body. When the rigid body rotates, the point object move on a circle of radius $r$.
If the point object moves a distance, $\Delta \ell$ on the circle, then its angular displacement, $\Delta \theta$ is defined as,
$\Delta \theta=\dfrac{\Delta \ell}{r}$
If you take any point on the rigid body, all of them have the same angular displacement. So, $\Delta \theta$ is the angular displacement of the rigid body. Angular displacement is a vector as it has a direction.
The SI unit of angular displacement is radian (rad.). The common unit of angular displacement or angle is degree ($^\circ$). We can find a relation between the radian and degree as follows.
When a point object makes one complete rotation, its angular displacement is $\Delta \theta= 360^\circ$. And, the distance traveled by the point object in one complete rotation is equal to the circumference of the circle. That is, $\Delta \ell = 2\pi r$. Substituting these in $\Delta \theta=\Delta \ell/r$, we get
$360^\circ=\dfrac{2\pi r}{r}\:rad.$
Canceling out the $r$'s,
$360^\circ=2\pi\:\:rad.$
or$\boxed{180^\circ=\pi\:\:rad.}$
This is the conversion factor between degrees and radians.Angular velocity
Angular velocity is the rate of change of angular displacement. It is a measure of how fast an object is rotating.If $\Delta \theta$ is the angular displacement of an object in a time interval, $\Delta t$, then the angular velocity of the object is
$\omega=\dfrac{\Delta {\theta}}{\Delta t}$
We use the greek letter omega ($\omega$) for angular velocity.
Unit of angular velocity is $rad./s.$
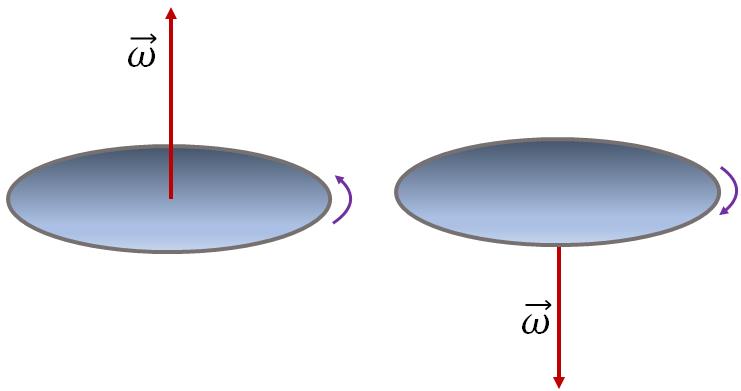
Angular velocity is a vector. The magnitude of angular velocity is called angular speed. Direction of angular velocity, $\vec \omega$ is determined by a rule called the right hand rule.It states that when you curl your fingers of the right hand around the rotation axis and point in the direction of rotation, then the thump points in the direction of the angular velocity.In the figure below you can see the rotating direction of a disc and the direction of its angular velocity.
Angular velocity and linear velocity
In translational motion, you studied about the velocity, $v$, and now in rotational motion, we have angular velocity, $\omega$. To distinguish one from the other, we call the velocity, $v$ as linear velocity. The two velocities are related as you will see below.Let us again consider a point of object of a right body. Assume in a small time interval, $\Delta t$, the point object travels a distance, $\Delta \ell$ on its circular path. So, the angular displacement of the point object is
$\Delta \theta=\dfrac{\Delta \ell}{r}$
Dividing by $\Delta t$,
$\dfrac {\Delta \theta}{\Delta t}=\dfrac{1}{r} \dfrac{\Delta \ell}{\Delta t}$
Left hand side is the angular velocity of the point object or the rigid body, $\omega$. And on the right hand side, $\Delta \ell/\Delta t$ is nothing but the linear velocity, $v$ of the point object. So we have,
$\omega =\dfrac{v}{r}$
(or)$\boxed{v=r\omega}$
The angular velocity and linear velocity are related by this equation.Note that the angular velocity of all the points of a rigid body is the same, but the linear velocity is different at different points as they are at different distance, $r$ from the axis of rotation.
Angular speed, period and frequency of rotation of a rigid body
The time for one full rotation of a rigid body is called the period, $T$ of rotation. In one full rotation, a point object of a rigid body travels a distance equal to the circumference of the circle. Therefore, the linear speed of the point object can be written as
$v=\dfrac{2\pi r}{T}$.
Substituting, $v=r\omega$, we get,
$r \omega =\dfrac{2\pi r}{T}$.
Canceling the $r$'s,
$\omega=\dfrac{2\pi}{T}$
The reciprocal of period is the frequency of rotation, that is, $f=1/T$. Substituting this in the equation, we get,
$\boxed{\omega=2\pi f}$
So, from the frequency of rotation of a rigid body, you can find its angular speed.
Angular acceleration
Angular acceleration is the rate of change of angular velocity.When there is a change in angular velocity of an object, there is an angular acceleration. We use the letter, alpha ($\alpha$) for angular acceleration. The angular acceleration of a rigid body is
$\alpha=\dfrac{\Delta \omega}{\Delta t}$.
where $\Delta \omega$ is the change in angular velocity of the rigid body in a time interval, $\Delta t$.
The SI unit of angular acceleration is $rad./s^2$.
Centripetal and tangential acceleration of a point object
When a rigid body rotates with a constant angular speed, then the speed (the linear speed) of each point object of the rigid body is constant. In this case, the point objects are in uniform circular motion. So, they have centripetal acceleration. The centripetal acceleration of a point object moving on a circle of radius $r$ is$a_c=\dfrac{v^2}{r}$
Substituting, $v=r\omega$, and simplifying, we get
$\boxed{a_c=r\omega^2}$
If the angular speed of the rigid body is not constant, then the speed (the linear speed) of the point objects are not constant. So, the objects will be in non-uniform circular motion. An object in non-uniform circular motion has another acceleration in addition to the centripetal acceleration. That acceleration is called the tangential acceleration. The tangential acceleration of an object is
$a_{tan}=\dfrac{\Delta v}{\Delta t}$
Note that when $v$ is constant, $a_{tan}=0$ and there will only be the centripetal acceleration.
From the equation, $v=r\omega$, we can write, $\Delta v=r\Delta \omega$. Substituting this in the previous equation,
$a_{tan}=r\dfrac{\Delta \omega}{\Delta t}$
Since, $\Delta \omega/\Delta t=\alpha$, we get,
$\boxed{a_{tan}=r\alpha}$
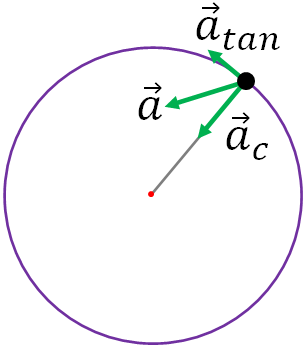
The direction of tangential acceleration is tangent to the circle as shown in the figure above. Note that the tangential acceleration is same as the acceleration in a translation motion. So, we call this as linear acceleration.
Since there are two accelerations for the point object in non-uniform circular motion, the net acceleration, $\vec a_{net}$ of the object is the vector sum of the two accelerations:
$\vec a_{net} = \vec a_c+\vec a_{tan}$
If you add the two vectors, you will get the direction of the net acceleration, $\vec a_{net}$ as shown in the figure above.
And, you will get the magnitude of the net acceleration,
$a_{net}=\sqrt{a_c^2+a_{tan}^2}$
Rotational kinematics
We used the 1-D kinematic equations to describe the translational or linear motion of objects. From these equations, we can obtain another set of equations to describe the rotational motion of objects. To get the equations, we need to substitute the following in the 1-D kinematic equations:$\Delta x=r \Delta \theta$; $v=r\omega$ ,and $a=a_{tan}=r\alpha$
After the substitution, you can cancel out the $r$ in the equations and you will get the following equations,
$\omega=\omega_0+\alpha t$
$\Delta \theta=\dfrac{1}{2}(\omega_o +\omega)t$
$\Delta \theta=\omega_0 t+\dfrac{1}{2}\alpha t^2$
$\omega ^2= \omega_0^2+2\alpha \Delta \theta$
These equations are called the rotational kinematic equations.
In the equations, $\omega_0$ is the initial angular velocity of the rigid body, $\omega$ is the velocity at time, $t$, you can also call this the final angular velocity, and $\Delta \theta$ is the angular displacement at time $t$. Note that $t=0$ is the initial time as in the 1-D kinematic equations.
It is important to note that the rotational kinematic equations are valid when the angular acceleration, $\alpha$ is constant. This is because the 1-D kinematic equations are valid for constant linear acceleration.
Torque
You know that in translational motion, a force accelerates an object. That is, a force is required for linear acceleration of an object. Now the question is what is needed for an angular acceleration of an object?. For that also a force is required. But not all forces can produce an angular acceleration. When a force is applied on a rotating object, the angular acceleration of a rotating object depends on three factors, (i) magnitude of the force, (ii) the direction of the force and (iii) the point of application of the force. A physical quantity that takes into account all these aspects is called, torque. So, a torque plays the role of force in rotational motion.To define torque, let us consider an object in the shape of a beam as shown in the figure below. Assume the object can rotate freely about the axis of rotation as in the figure. And, you are applying a force, $\vec F$ on the object to rotate it as shown.
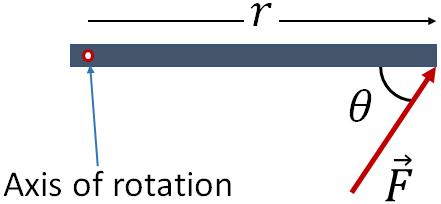
The magnitude of torque, $\tau$ exerted on the object by the force is defined as
$\tau=rF\sin \theta$
where $r$ is the distance between the axis of rotation (also called pivot) and the point where the force is applied; and $\theta$ is the angle between the force and a line joining the pivot and the point of application of the force.Now, draw a perpendicular line from the pivot to the force vector (you can extend the force line if needed). The length of this line is $r_\perp$, which is called the lever arm or the moment arm.
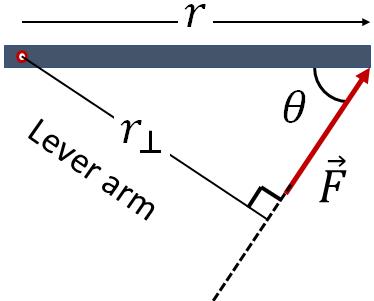
From the right angled triangle in the figure above, we can write,
$r_\perp = r \sin\theta$
So, the torque can also be written as
$\tau=r_\perp F$
Torque is also called moment or moment of force. A net torque on an object rotates the object in rest or changes the angular velocity if the object is already in rotational motion.
Direction of torque
Torque is a vector. Its direction is determined by another right hand rule: stretch your fingers in the direction from the pivot to the point where the force is being applied, then swirl your fingers in the direction of the force, now the thumb points to the direction of the torque.Sign convention for torques
When you apply a torque on an object, it tends to rotate the object. A torque can rotate an object either in the clockwise or in the counter clockwise direction. So, if there are more than one torque acting on an object, we need a sign convention to add them to find the net torque. We use the following sign convention. If a force tends to rotate the object in the counter clockwise direction, then the torque by that force is positive, and the torque is negative, if the force tends to rotate the object in the clockwise direction.Torque on a rotating point object
Again, consider a point object in a rigid body. To rotate the point object, you need to apply a force on the object. But only the force or force component tangent to the circle can rotate the object.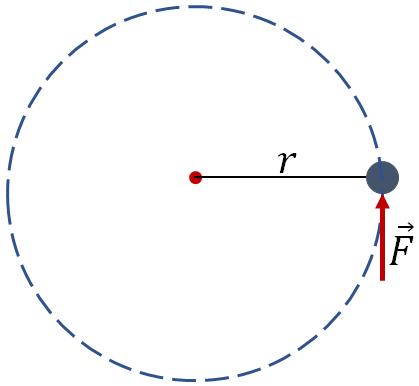
$\tau=rF$.
where $r$ is the radius of the circle.
Since the force ccelerate the object tangentially, we have
$F=ma_{tan}=mr\alpha$
Substituting this in the torque equation,
$\tau=mr^2\alpha$.
This is the equation for the torque on a point object.
Torque on a rotating rigid body
We have the torque acting on a rotating point object. By using that we can find the torque on a rotating rigid body. Again, assume the rigid body is made up of a large number of point objects. And, there are $n$ number of point objects. When the rigid body rotates, all point objects rotate with same angular acceleration, but on circles of different radii. Let $m_1, m_2, m_3, ..., m_n$ are the masses of the point objects and $r_1, r_2, r_3, ..., r_n$ are the radii of their circular paths. Now, if you add the torque on all point objects, you will get the torque on the rigid body. The torque on the rigid body is therefore,$\tau=m_1r_1^2\alpha+m_2r_2^2\alpha+...m_nr_n^2\alpha$
$\tau=(m_1r_1^2+m_2r_2^2+...m_nr_n^2)\alpha$
or$\tau=I\alpha$
where $I = m_1r_1^2+m_2r_2^2+...m_nr_n^2$
$I$ is called the moment of inertia of the rigid body about the axis of rotation.
The moment of inertia of a rigid body depends on the mass, shape and the axis of rotation. With the use of calculus, we can find the moment of inertia of rigid bodies of different shapes.
The moment of inertia of objects of different shapes and axis of rotation are given in the table below. $M$ in the table is the mass of the object
| Object | Axis of rotation |
Moment of inertia |
|---|---|---|
|
Uniform sphere 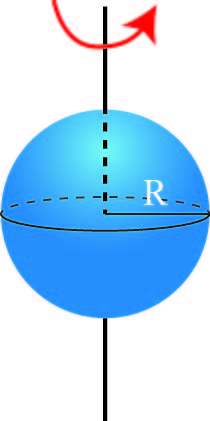
|
Through center |
$\dfrac{2}{5}MR^2$ |
|
Solid cylinder 
|
Through center |
$\dfrac{1}{2}MR^2$ |
|
Hollow cylinder 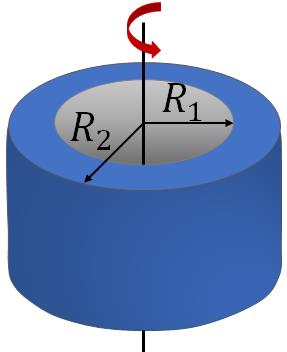
|
Through center |
$\dfrac{1}{2}M\left(R_1^2+R_2^2\right)$ |
|
Long 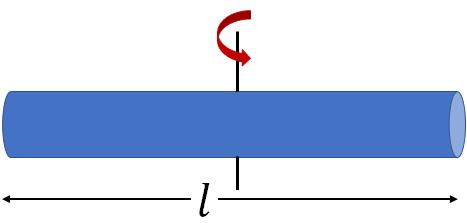
|
Through center |
$\dfrac{1}{12}Ml^2$ |
|
Long 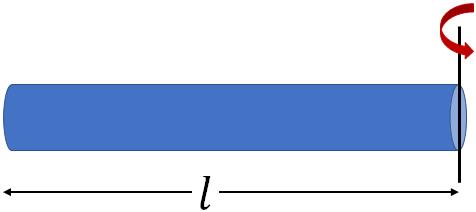
|
Through one end |
$\dfrac{1}{3}Ml^2$ |
Thin hoop
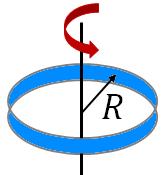
|
Through center |
$MR^2$ |
|
Thin hoop 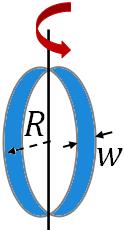
|
Through central diameter |
$\dfrac{1}{2}MR^2+\dfrac{1}{12}Mw^2$ |
|
Rectangular 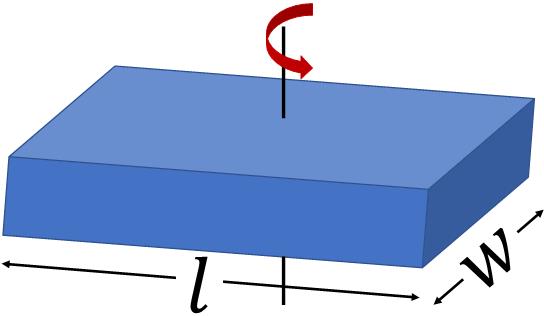
|
Through center |
$\dfrac{1}{12}M\big(l^2+w^2\big)$ |
Rotational kinetic energy
An object in rotation has kinetic energy, like an object in translational motion. To find the kinetic energy of a rotating object, we use the same strategy that we used to find the torque on a rigid body. Assume the rigid body is made up of large number of point objects. As the body rotates each point object rotates with same angular velocity but with different linear velocities because of different radius. Total kinetic energy of the body is the sum of the kinetic energies of the point objects. Therefore,$KE_{rot}=\dfrac{1}{2}m_1v_1^2+\dfrac{1}{2}m_2v_2^2+...+\dfrac{1}{2}m_nv_n^2$.
where $\omega$ is the angular velocity of the rigid body.
Substituting $v=r\omega$, we have
$KE_{rot}=\dfrac{1}{2}m_1r_1^2\omega^2+\dfrac{1}{2}m_2r_2^2\omega^2+...+\dfrac{1}{2}m_nr_n^2\omega^2$.
$KE_{rot}=\dfrac{1}{2}(m_1r_1^2+m_2r_2^2+...+m_nr_n^2)\omega^2$.
or$KE_{rot}=\dfrac{1}{2}I\omega^2$
where $I$ is the moment of inertia of the object about the axis of rotation.
With this equation, you can find the rotational kinetic energy of a rotating rigid body.
Kinetic energy of a rolling object
If an object undergoes both rotational and translational motion on a surface, then we call that rolling motion. If you ride a bike, the wheels of the bike are in rolling motion as they rotate about their axle and also translate from one place to another. A rolling object has both translational and rotational kinetic energy. Further, if you roll an object, it will rotate about its center of mass. Therefore, total kinetic energy of a rolling object is$KE=\dfrac{1}{2}mv^2+\dfrac{1}{2}I_{cm}\omega^2$
where $I_{cm}$ is the moment of inertia of the object about its center of mass.
Work and power in rotational motion
Work in rotation
Torque does work on a rotating object in the same way a force does work on an object that makes linear displacement.
To derive the equation for work by torque, we consider a wheel with a rope around its rim. And assume, you are pulling the rope with a force of magnitude $F$, so that the wheel moves a distance $d$. Now the work done by the force is
$W=F\, d$.
We can relate the distance $d$ with the rotating angle, $\Delta \theta$ of the wheel by
$d=r\Delta \theta$
Substituting this in the above equation, you get
$W=F\, r \Delta \theta$
$F\, r$ is nothing but the torque on the wheel, so we can write
$W=\tau \Delta \theta$
Thus, if a torque on an object rotate the object, a work is done on the object by the torque.
Power in rotation
You learned that power is the amount of work done per unit time. If $W$ is the amount of work done in a time $\Delta t$, then the power generated is$P=\dfrac{W}{\Delta t}$
Substituting, $W=\tau \Delta \theta$,
$P=\tau \dfrac{\Delta \theta}{\Delta t}$
Since $\dfrac{\Delta \theta}{\Delta t}=\omega$, the power generated by torque is
$P=\tau \omega$
Angular momentum
Angular momentum in rotational motion is analogous to the linear momentum in translational motion. Angular momentum $(L)$ of a rotating object is defined as,$L=I\omega$
where $I$ is the angular momentum about the axis of rotation of the object.Unit of angular momentum is $kg.m^2/s$.
Since the angular momentum is proportional to the angular velocity, its direction is same as the angular velocity.
Torque and angular momentum
We have the relation between the torque and the angular acceleration of a rigid body,
$\tau=I\alpha$.
$=I\dfrac{\Delta \omega}{\Delta t}$
$=\dfrac{\Delta (I\omega)}{\Delta t}$
(or)$\tau=\dfrac{\Delta L}{\Delta t}$
i.e., the torque is just the rate of change of angular momentum.
When you compare the angular momentum with linear momentum, you see that force is the rate of change of linear momentum, and torque is the rate of change of angular momentum.
Conservation of angular momentum
You learned in linear momentum that when there is no net external force acting on a system (an isolated system), the linear momentum is conserved.Angular momentum is also conserved when there is no net torque acting on a rigid body as you see below.
We have,
$\tau=\dfrac{\Delta L}{\Delta t}$
Putting, $\tau=0$,
$\dfrac{\Delta L}{\Delta t}=0$
$\Delta L=0$
or$L=$ constant
That is the angular momentum is constant when there is no net torque acting on a rotating object. i.e., the angular momentum of a rotating object is conserved.
So, if $L_1$ and $L_2$ are the initial and final angular momenta of a rotating object or a system, then
$L_1=L_2$
