Momentum
Momentum is an important concept in physics that is very useful to study the motion of objects involving collision. When an object is in motion, we say that the object has momentum. Momentum in physics has the same meaning as in real life momentum. In this page, you are going to learn about the following, definition of momentum, isolated system, the law of conservation of momentum, impulse, types of collisions, 1-D and 2-D collisions, and the center of mass.Linear momentum or momentum
Momentum, $\vec p$ of an object is defined as$\vec p=m\vec v$
where $m$ is the mass of the object, and $\vec v$ is its velocity.
Since velocity is a vector, momentum is a vector. The direction of momentum is the direction of the object's velocity. The momentum, $\vec p$ is also called linear momentum or translational momentum.If the velocity of an object is zero, then it has no momentum.
Unit of momentum:To find the unit of momentum, we need to multiply the unit of mass and the unit of velocity. The SI unit of momentum is $kg.m/s$ or $N.s$.
Force and momentum
To change the momentum of an object, we need to change the velocity of the object. To change the velocity, a force needs to be applied on the object. So, to change the momentum of an object, a force must be applied on the object. We can derive an equation that relates force and momentum change, by using Newton's second law.Assume an object is moving with some (initial) velocity, $\vec v_i$. Now, let us apply a net force, $\vec F$ on the object for a time period, $\Delta t$. The force changes the velocity of the object, let the new velocity be $\vec v_f$.
Writing Newton's second law,
$\vec F=m\vec a$
$=m\dfrac{\Delta \vec v}{\Delta t}$
$=m\dfrac{\vec v_f-\vec v_i}{\Delta t}$
$=\dfrac{m\vec v_f-m\vec v_i}{\Delta t}$
$=\dfrac{\vec p_f-\vec p_i}{\Delta t}$
where $\vec p_i=m \vec v_i$ and $\vec p_f = m \vec v_f$ are the initial and the final momentum of the object. The initial momentum is the momentum of the object before the force is applied and the final momentum is momentum just after the force is applied.
Since, $\vec p_f-\vec p_i=\Delta \vec p$, the change in momentum of the object, we get,
$\vec F=\dfrac{\Delta \vec p}{\Delta t}$
i.e., the force applied on an object is just the change in momentum of the object divided by the time the force acts on the object. Or the force on an object is equal to the rate of change of momentum of the object. This equation is actually the original form of Newton's second law as formulated by Newton, but now we use the $\vec F = m\vec a$ form as the second law.
The law of conservation of momentum
Isolated system
A system is a group of two or more objects. If the net external force acting on a system is zero, we call that an isolated system. So, no external force affect an isolated system. The objects of an isolated system can collide with one another. During the collision, one object exerts a force on another object. So, the object of an isolated system can be exerted by a force from another object in the system, but not from the outside of the system.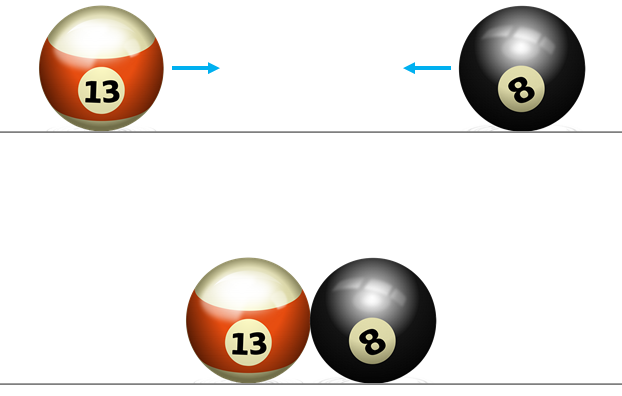
In the figure above, there are two billiard balls move toward each other and involve in a collision. We can consider the two balls as a system. During the collision, the red ball exerts a force on the black ball and the black ball exerts a force on the red ball. These forces are the internal forces of the system as both the balls are part of the system. Is there any external force on the system? There are 3 forces acting on the system. On each ball, there is a force of gravity acting downwards and a normal force by the surface acting vertically upwards. These two forces balances. So, there is no net external force acting on the objects in the vertical direction. In the horizontal direction, there is a force of friction acting on the balls. So, there is a net horizontal force acting on each object. Thus, the net force on the system is not zero due to the friction. If the surface is smooth and has no friction, then the system is an isolated system.
Law of conservation of momentum
We can show that the total momentum of an isolated system is conserved. That is, if the objects of an isolated system is involved in a collision, the total momentum of the system before collision is equal to the total momentum after the collision. This is called the law of conservation of momentum. Total momentum of the system is the sum of the momenta of the objects of the system.The figure below shows an isolated system of two objects, object 1 and object 2. The objects are in motion, and involve in a collision. Let $\vec p_1$ and $\vec p_2$ are the momenta of object 1 and object 2 before collision. And $\vec p_1'$ and $\vec p_2'$ are the momenta after the collision.
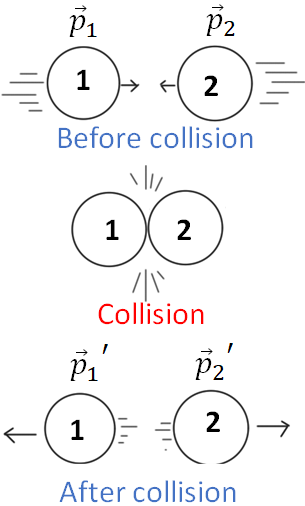
The total momentum of the system before the collision is $\vec p_1+\vec p_2$ and the total momentum after the collision is $\vec p_1'+\vec p_2',$. According to the law of conservation of momentum, the total momentum before the collision is equal to the total momentum after the collision. Therefore,
$\vec p_1+\vec p_2=\vec p_1'+\vec p_2'$.
The proof of the law of conservation of momentum is given in a separate page: the law of conservation of momentum.
Note that, momentum is conserved only in an isolated system. In an isolated system, there is no net external force acting on the objects of the system. In real world collision problems, friction is the external force that acts on objects moving on surfaces. But friction requires some time to affect the motion of the objects. So, if we consider the motion of the objects immediately before and immediately after collision, then we can ignore the friction and can consider a system as an isolated system. And, the law of conservation of momentum holds.
One dimensional collision
In a one dimensional (1-D) collision, the objects involve in the collision move on a straight line path before and after the collision.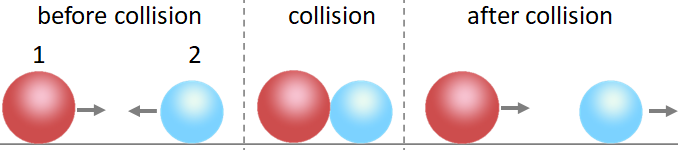
The figure above shows the collision of two objects, object 1 and object 2. This is a 1-D collision as before and after the collision, the path of the objects is the same and a straight line. Since the objects are in 1-D motion, we ignore the vector symbol for the momenta of the objects. We just need to be careful about the sign of the vectors.
If $m_1$ and $m_2$ are the masses of the objects 1 and 2; $v_1$ and $v_2$ are the velocities of the objects 1 and 2 before the collision; and $v_1'$ and $v_2'$ are the velocities after the collision, then
the total momentum of the system before the collision is $=m_1v_1+m_2v_2$
and
the total momentum after the collision $=m_1v_1'+m_2v_2'$.
The above two momenta are equal according to the law of conservation of momentum, therefore
$\boxed{m_1v_1+m_2v_2=m_1v_1'+m_2v_2'}$
This is the law of conservation of momentum for a collision in a 1-D motion. Note that you need to put the appropriate sign when using this equation. For example, if you consider to the right as positive direction, then the velocity of an object moving in that direction is positive and the velocity of the object moving to the left is negative.
Impulse
When two objects are in collision, there is a brief period of time, the objects exert force on one another. The force on an object multiplied with the impact time is called the impulse.Impulse imparted to an object by a force $(\vec F)$ is
$Impulse=\vec F \Delta t$
By using the force-momentum relation, $\vec F=\dfrac{\Delta \vec p}{\Delta t}$, we can write,
$Impulse=\Delta \vec p$
i.e., impulse is just the change in momentum. So you can use either of the above formula to find the impulse.Impulse is a vector and its direction is the direction of the force.
Applying a larger force for a short time produces the same impulse (or change in momentum) as applying a smaller force for a long time.
Types of collisions
There are two types of collisions: elastic and inelastic. In all collisions, the momentum is conserved. In an elastic collision, kinetic energy is also conserved.Elastic collision
In an elastic collision, momentum and kinetic energy, both are conserved. Collision between hard objects is generally elastic. Some of the examples of elastic collision are collision between billiard balls, collision between atoms or molecules. During an elastic collision, no heat or other energy is produced, so there is no loss in kinetic energy.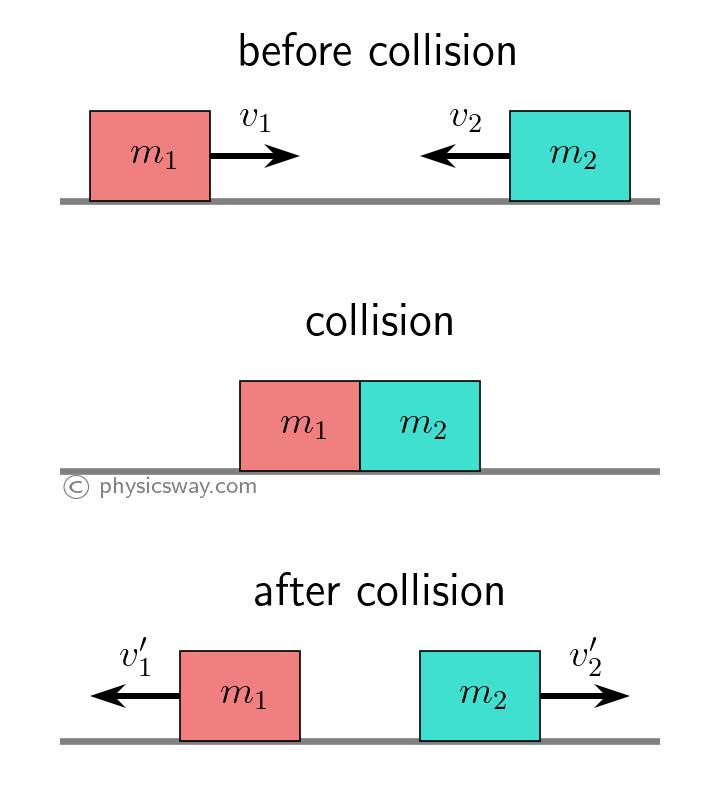
The figure above shows two objects in a 1-D elastic collision. The mass of object 1 is $m_1$ and that of object 2 is $m_2$. The velocities of the objects before and after the collision are shown in the figure.
When objects involve in a 1-D elastic collision, we have two equations to solve, one is the law of conservation of momentum and the other is for the conservation of kinetic energy:
$m_1v_1+m_2v_2=m_1v_1'+m_2v_2'$.
and$\dfrac{1}{2}m_1v_1^2+\dfrac{1}{2}m_2v_2^2=\dfrac{1}{2}m_1v_1'^2+\dfrac{1}{2}m_2v_2'^2$
The left hand side is the total kinetic energy of the objects before the collision and the right hand side is that after the collision.
To solve problems involving elastic collision, you need to use these two equations. But solving these two equations are time consuming. But we have another simple equation that we can obtain from the above two equations. That is,
$v_1-v_2=-(v'_1-v'_2)$
You can find the derivation of this equation in the page: elastic collision equations.
We use this equation and the first equation (the momentum conservation equation) to solve problems involving 1-D elastic collision.
Inelastic collision
In an inelastic collision, only the momentum is conserved, kinetic energy is not conserved. There is a loss or gain in kinetic energy of the system occurs in an inelastic collision. Further an inelastic collision can be, completely inelastic or partially inelastic. In a completely inelastic collision, the colliding objects stick together, but in a partially inelastic collision, the objects do not stick together but move separately after the collision.Two dimensional collision
In a two dimensional (2-D) collision, the paths of the objects before and after the collision are not on a line.Let us consider the following 2-D collision involving a system two objects: object 1 of mass $m_1$and object 2 of mass $m_2$. Object 1 is moving on the positive $x$ direction with speed $v_1$ toward object 2 that is at rest.
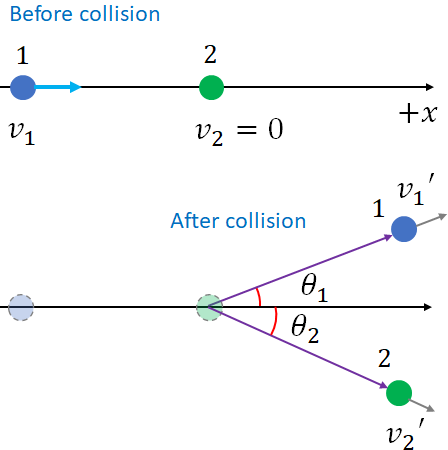
Then, object 1 collides with object 2, and after the collision, object 1 move at an angle $\theta_1$ above the $x$ axis with speed $v_1'$ and object 2 at an angle $\theta_2$ below the $x$ axis with speed $v_2'$.
We describe the collision with momentum vectors. Since $x$ and $y$ components of a momentum are independent of each other, momentum is conserved along the $x$ axis and along the $y$ axis separately. So, we will have two momentum conservation equations, one for the $x$ direction and the other for the $y$ direction.
i.e., $p_x=p_x'$ and $p_y=p_y'$
where $p_x$ and $p_y$ respectively are the $x$ and the $y$ the components of the total momentum of the system before the collision, and $p_x'$ and $p_y'$ are those after the collision.
First let us consider the momentum before the collision.
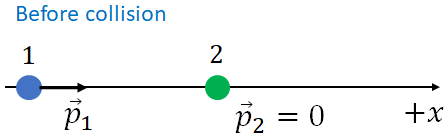
The momentum of object 1, $\vec p_1$ is on the $x$ axis as the object 1 moves along the $x$ axis. The magnitude of $\vec p_1$ is
$p_1=m_1v_1$
Since $\vec p_1$ is on the $+x$ axis, we have
$p_{1x}=m_1v_1$ and $p_{1y}=0$
Since the object 2 is in rest, its momentum, $\vec p_2=0$. So we have
$p_{2x}=0$ and $p_{2y}=0$
Adding the $x$ components of the momenta of object 1 and 2, we get
$p_x=m_1v_1$
And, adding the $y$ components of the momenta of object 1 and 2, we get
$p_y=0$
Now, let us consider the momentum after the collision.
The momenta, $\vec p_1'$ and $\vec p_2'$ of the object 1 and the object 2 after the collision are shown in the figure below. The magnitudes of the momenta are
$p_1'=m_1v_1'$ and $p_2'=m_2v_2'$
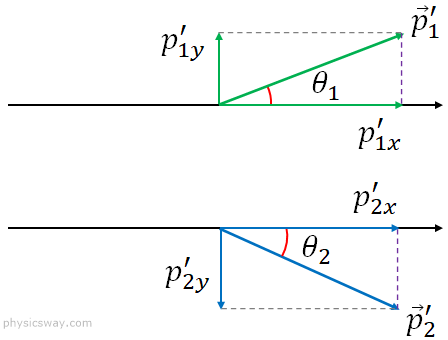
$p_{1x}'=m_1v_1'\cos\theta_1$ and $p_{1y}'=m_1v_1'\sin\theta_1$
And for the object 2,
$p_{2x}'=m_2v_2'\cos\theta_2$ and $p_{2y}'=-m_2v_2'\sin\theta_2$
Adding the $x$ components of the momenta of the objects together and the $y$ components together, we get
$p_x'=m_1v_1'\cos\theta_1+m_2v_2'\cos\theta_2$ and
$p_y'=m_1v_1'\sin\theta_1-m_2v_2'\sin\theta_2$
Applying the law of conservation of momentum along the $x$ axis ($p_x=p_x'$)and along the $y$ axis ($p_y=p_y'$), we get,
$m_1v_1=m_1v_1'\cos\theta_1+m_2v_2'\cos\theta_2$
and$0=m_1v_1'\sin\theta_1-m_2v_2'\sin\theta_2$
These are the two equations that you will use to solve problems for the 2-D collision.
Center of mass
In the figure below, there is a rock, what is the position of the rock?
If you have a spherical object, then we consider its center as the position of the object. In 2-D, if the object is of regular shape such as a circle, square or a rectangle, we can find a center point by drawing lines of symmetry and the point of intersection is the center point. This point we call the center of mass.
Center of mass is the average position of an object's or a system’s mass. For a sphere, center of mass is the center of the sphere.
How to find the center of mass?
In the following figure, you have a system of two spherical objects of mass $m_1$ and $m_2$ connected together by a light rod of negligible mass, what is the center of mass of the system?.

In three dimensions (3-D), a point is described by three coordinates: $(x, y, z)$. Since the center of mass is a point, we write the position of the center of mass as
$r_{cm}=(x_{cm}, y_{cm}, z_{cm})$
where, $x_{cm}$, $y_{cm}$,and $z_{cm}$ are the $x$, $y$ and the $z$ coordinates of the center of mass.
If the position of the center of object 1 is $(x_1, y_1, z_1)$ and that of object 2 is $(x_2, y_2, z_2)$, then
$x_{cm}=\dfrac{m_1x_1+m_2x_2}{m_1+m_2}$
$y_{cm}=\dfrac{m_1y_1+m_2y_2}{m_1+m_2}$
and$z_{cm}=\dfrac{m_1z_1+m_2z_2}{m_1+m_2}$
The above equations can be extended if there are more than two objects. For example, if there are 4 objects, then there will be two more terms in the numerator and in the denominator of the equations above.
Now, the question is how to find the center of mass of a irregular shape object, like the rock?
If you have an irregular object such as a rock, then to find the center of mass, assume the object is made up of a large number of tiny regular shape objects of same mass. Each tiny object has different position, and the average of positions of those tiny objects will be the center of mass of the object.
Why the center of mass is important?
For a rigid body, the center of mass is an important parameter. If you consider the gravitational force between two objects of spherical shape, then for the distance between the objects, you measure the center-to-center distance between the two objects. But if the two objects are of irregular shapes, then the distance you will measure will be the distance between the center of mass of the objects.Center of mass is also called center of gravity, although the definition of center of gravity is different than the center of mass. But in most cases center of gravity and the center of mass are the same. As you see in the figure below, the center of mass is the balancing point.
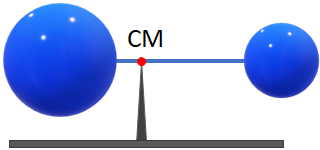
The center of mass is closest to where there is more mass present. So, you can realize that the mass to the left of the center of mass and the mass to the right are not the same.
